第21题

已知：如图，在△ABC中，AB=AC，AE是角平分线，BM平分∠ABC交AE于点M，经过B，M两点的⊙O交BC于点G，交AB于点F，FB恰为⊙O的直径．

（1）求证：AE与⊙O相切；

参考答案：见解析

解析：

【考点】切线的判定；等腰三角形的性质；相似三角形的判定与性质；解直角三角形．

【专题】几何综合题．

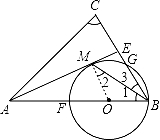
【分析】（1）连接OM，证明OM∥BE，再结合等腰三角形的性质说明AE⊥BE，进而证明OM⊥AE；

（2）结合已知求出AB，再证明△AOM∽△ABE，利用相似三角形的性质计算．

【解答】（1）证明：连接OM，则OM=OB

∴∠1=∠2

∵BM平分∠ABC

∴∠1=∠3

∴∠2=∠3

∴OM∥BC

∴∠AMO=∠AEB

在△ABC中，AB=AC，AE是角平分线

∴AE⊥BC

∴∠AEB=90°

∴∠AMO=90°

∴OM⊥AE

∵点M在圆O上，

∴AE与⊙O相切；

（2）解：在△ABC中，AB=AC，AE是角平分线

∴BE=BC，∠ABC=∠C

∵BC=4，cosC=

∴BE=2，cos∠ABC=

在△ABE中，∠AEB=90°

∴AB==6

设⊙O的半径为r，则AO=6﹣r

∵OM∥BC

∴△AOM∽△ABE

∴

∴

解得

∴⊙O的半径为．

【点评】本题是小综合题，考查等腰三角形，平行线，角平分线，直线和圆的位置关系，相似三角形等知识点．

第22题

自2010年6月1日起我省开始实施家电以旧换新政策，消费者在购买政策限定的新家电时，每台新家电用一台同类的旧家电换取一定数额的补贴．为确保商家利润不受损失，补贴部分由政府提供，其中三种家电的补贴方式如下表：

参考答案：见解析

解析：

【考点】一次函数的应用．

【专题】优选方案问题．

【分析】（1）由于电视机每台售价4300元，其10%为430元，超过400元，故其补贴额为400元；而洗衣机、冰箱的补贴额度不超过400元，故按照其销售价格的10%计算即可．

（2）根据商场决定购进每种家电不少于30台，即电视机和洗衣机数x≥30台；冰箱100﹣2x≥30台，列出不等式组解答即可．

【解答】解：（1）y=400x+1800×10%x+2400×10%（100﹣2x）=100x+24000

商场所获利润：W=400x+300x+400（100﹣2x）

=﹣100x+40000．

（2）根据题意得，

解得30≤x≤35，

因为x为整数，所以x=30，31，32，33，34，35，因此共有6种进货方案．

对于W=﹣100x+40000，

∵k=﹣100＜0，30≤x≤35，

∴当x=30时，W有最大值，

所以当购进30台电视，30台洗衣机，40台电冰箱时商场将获得最大的利润．

因此政府的补贴为y=100×30+24000=27000元．

【点评】此题将一元二次方程与不等式组相结合，以实际问题为载体，体现了数学的实用价值，也对同学们阅读理解能力提出了较高的要求，是考试中常见常新的题目．

第23题

如图1，在正方形ABCD中，点M、N分别在AD、CD上．

（1）若∠MBN=45°且∠ABM=∠CBN，则易证　　　　　　．（选择正确答案填空）

参考答案：见解析

解析：

【考点】四边形综合题．

【专题】综合题．

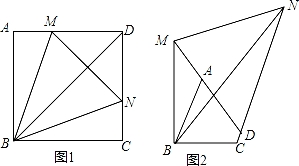
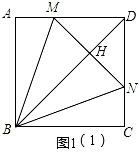
【分析】（1）设BD于MN交于点H，如图1（1），根据正方形的性质得∠ABH=∠CBH=45°，BA=BC，由于∠MBN=45°，∠ABM=∠CBN，则∠ABM=∠HBM=∠HBN=∠CBN，再证明△ABM≌△CBN得到BM=BN，AM=CN，接着根据等腰三角形的性质可判断BH⊥MN，于是根据角平分线的性质得MA=MH，NH=NC，所以有MN=AM+CN；

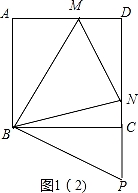
（2）把△BAM绕点B顺时针旋转90°得到△BCP，如图1（2），根据旋转的性质得BM=BP，AM=CP，∠MBP=90°，∠BCP=∠A=90°，再证明点P在DC的延长线上，则NC+CP=NP，利用∠MBN=∠ABC=45°得到∠NBP=45°，接着可证明△BNM≌△BNP，则MN=NP，于是有MN=CP+CN=AM+CN；

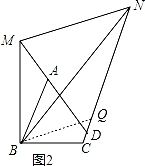
【拓展】如图2，由于∠ABC+∠ADC=180°，根据四边形内角和得到∠BAD+∠BCD=180°，则∠BAM=∠BCD，根据旋转的定义，可把△BAM绕点B顺时针旋转90°得到△BCQ，则根据旋转的性质得∠BAM=∠BCQ，BM=BQ，∠MBQ=∠ABC，则∠BCQ=∠BCD，则可判断点Q在CN上得到CN=CQ+MQ=AM+NQ，然后证明△BMN≌△BQN得到MN=QN，则CN=AM+MN．

【解答】（1）解：设BD于MN交于点H，如图1（1），

∵BD为正方形ABCD的正方形，

∴∠ABH=∠CBH=45°，BA=BC，

∵∠MBN=45°，∠ABM=∠CBN，

∴∠ABM=∠HBM=∠HBN=∠CBN，

在△ABM和△CBN中

，

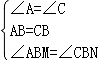∴△ABM≌△CBN，

∴BM=BN，AM=CN，

而∠HBM=∠HBN，

∴BH⊥MN，

∴MA=MH，NH=NC，

∴AM=MH=HN=NC，

∴MN=AM+CN；

故答案为③；

（2）解：在（1）中线段MN、AM、CN之间的数量关系仍然成立．理由如下：

把△BAM绕点B顺时针旋转90°得到△BCP，如图1（2），

∴BM=BP，AM=CP，∠MBP=90°，∠BCP=∠A=90°，

∵∠BCP+∠BCN=180°，

∴点P在DC的延长线上，

∴NC+CP=NP，

∵∠MBN=∠ABC=45°，

∴∠NBP=45°，

在△BNM和△BNP中

，

∴△BNM≌△BNP，

∴MN=NP，

∴MN=CP+CN=AM+CN；

【拓展】解：如图2，∵∠ABC+∠ADC=180°，

∴∠BAD+∠BCD=180°，

而∠BAD+∠BAM=180°，

∴∠BAM=∠BCD，

∵AB=BC，

∴把△BAM绕点B顺时针旋转90°得到△BCQ，

∴∠BAM=∠BCQ，BM=BQ，∠MBQ=∠ABC，

∴∠BCQ=∠BCD，

∴点Q在CN上，

∴CN=CQ+MQ=AM+NQ，

∵∠MBN=∠ABC，

∴∠MBN=MBQ，[来源:Zxxk.Com]

∴∠MBN=∠QBN，

在△BMN和△BQN中[来源:Zxxk.Com]

，

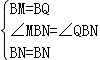∴△BMN≌△BQN，

∴MN=QN，

∴CN=AM+MN，

即MN=CN﹣AM．

【点评】本题考查了四边形的综合题：熟练掌握正方形的性质和旋转的性质；灵活应用全等三角形的判定与性质解决线段相等的问题；解决本题的关键是构建全等三角形．

第24题

一元二次方程x（2x+3）=5的常数项是（　　）

A.﹣5

B.2

C.3

D.5

参考答案：A

解析：

【考点】一元二次方程的一般形式．

【分析】方程整理为一般形式后，找出常数项即可．

【解答】解：方程整理得：2x²+3x﹣5=0，

则常数项为﹣5，

故选A．

第25题

如图所示的几何体的左视图是（　　）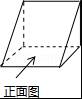

A.

B.

C.

D.

参考答案：A

解析：

【考点】简单几何体的三视图．

【分析】找到从几何体的左边看所得到的图形即可．

【解答】解：从几何体的左边看可得直角三角形，

故选：A．

第26题

有三张正面分别写有数字﹣1，1，2的卡片，它们背面完全相同，现将这三张卡片背面朝上洗匀后随机抽取一张，以其正面数字作为a的值，然后再从剩余的两张卡片随机抽一张，以其正面的数字作为b的值，则点（a，b）在第二象限的概率为（　　）

A.

B.

C.

D.

参考答案：B

解析：

【考点】列表法与树状图法；点的坐标．

【分析】画出树状图，然后确定出在第二象限的点的个数，再根据概率公式列式进行计算即可得解．

【解答】解：根据题意，画出树状图如下：

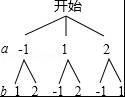
一共有6种情况，在第二象限的点有（﹣1，1）（﹣1，2）共2个，

所以，P==．

故选B．

第27题

下列关于矩形的说法，正确的是（　　）

A.对角线相等的四边形是矩形

B.对角线互相平分的四边形是矩形

C.矩形的对角线互相垂直且平分

D.矩形的对角线相等且互相平分

参考答案：D

解析：

【考点】矩形的判定与性质．

【分析】根据定义有一个角是直角的平行四边形叫做矩形．矩形的性质：

  1．矩形的四个角都是直角

  2．矩形的对角线相等

  3．矩形所在平面内任一点到其两对角线端点的距离的平方和相等

  4．矩形既是轴对称图形，也是中心对称图形（对称轴是任何一组对边中点的连线）．

  5．对边平行且相等

  6．对角线互相平分，对各个选项进行分析即可．

【解答】解：A、因为对角线相等的平行四边形是矩形，所以本选项错误；

B、因为对角线互相平分且相等的四边形是矩形，所以本选项错误；

C、因为矩形的对角线相等且互相平分，所以本选项错误；

D、因为矩形的对角线相等且互相平分，所以本选项正确．

故选：D．

第28题

小明乘车从广州到北京，行车的平均速度y（km/h）和行车时间x（h）之间的函数图象（　　）

A.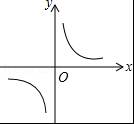

B.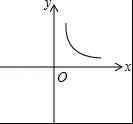

C.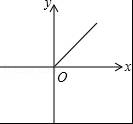

D.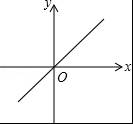

参考答案：B

解析：

【考点】反比例函数的应用；反比例函数的图象．

【分析】根据时间x、速度y和路程s之间的关系，在路程不变的条件下，得y=，则y是x的反比例函数，且x＞0．

【解答】解：由题意可得：y=（x＞0），

故y是x的反比例函数．

故选：B．

第29题

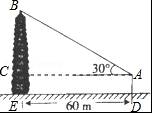
如图，小强和小明去测量一座古塔的高度，他们在离古塔60m的A处，用测角仪测得古塔顶的仰角为30°，已知测角仪高AD=1.5m，则古塔BE的高为（　　）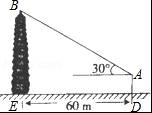

A.（20﹣1.5）m

B.（20+1.5）m

C.31.5m

D.28.5m

参考答案：B

解析：

【考点】解直角三角形的应用-仰角俯角问题．

【分析】作AC⊥BE于点C．则CE=AD，AC=DE．在直角△ABC中选择适当的三角函数求出BC即可得解．

【解答】解：过点A作AC⊥BE于点C．

根据题意有：AC=DE=60，CE=AD=1.5．

∴BC=AC×tan30°=20．

故古塔BE的高为BC+CE=（20+1.5）m．

故选B．

第30题

若两个相似三角形的面积比为2：3，那么这两个三角形的周长的比为（　　）

A.4：9

B.2：3

C.：

D.3：2

参考答案：C

解析：

【考点】相似三角形的性质．

【分析】根据相似三角形周长的比等于相似比、相似三角形面积的比等于相似比的平方解答即可．

【解答】解：∵两个相似三角形的面积比为2：3，

∴这两个三角形的相似比为：，

∴这两个三角形的周长的比为：，

故选：C．

第31题

如图，正方形OABC的两边OA、OC分别在x轴、y轴上，点D（5，3）在边AB上，以C为中心，把△CDB旋转90°，则旋转后点D的对应点D′的坐标是（　　）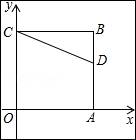

A.（2，10）

B.（﹣2，0）

C.（2，10）或（﹣2，0）

D.（10，2）或（﹣2，0）

参考答案：C

解析：

【考点】坐标与图形变化-旋转．

【分析】分顺时针旋转和逆时针旋转两种情况讨论解答即可．

【解答】解：∵点D（5，3）在边AB上，

∴BC=5，BD=5﹣3=2，

①若顺时针旋转，则点D′在x轴上，OD′=2，

所以，D′（﹣2，0），

②若逆时针旋转，则点D′到x轴的距离为10，到y轴的距离为2，

所以，D′（2，10），

综上所述，点D′的坐标为（2，10）或（﹣2，0）．

故选：C．

第32题

在Rt△ABC中，∠C=90°，BC=3，AB=12，sinA=　　．

参考答案：1/4

解析：

【考点】锐角三角函数的定义．

【分析】根据正弦的概念计算即可．

【解答】解：sinA==，

故答案为：．

第33题

我们知道，平行光线所形成的投影称为平行投影，当平行光线与投影面　　，这种投影称为正投影．

参考答案：垂直

解析：

【考点】平行投影．

【分析】根据正投影定义解答．

【解答】解：在平行投影中，当投影线垂直于投影面时，这种投影叫正投影，

故答案为：垂直．

第34题

已知关于x的一元二次方程x²+bx+b﹣1=0有两个相等的实数根，则b的值是　　．

参考答案：2

解析：

【考点】根的判别式．

【分析】根据方程有两个相等的实数根，得到根的判别式的值等于0，即可求出b的值．

【解答】解：根据题意得：△=b²﹣4（b﹣1）=（b﹣2）²=0，

则b的值为2．

故答案为：2

第35题

反比例函数y=的图象，当x＞0时，y随x的增大而增大，则k的取值范围是　　．

参考答案：k＜3

解析：

【考点】反比例函数的性质．

【分析】先根据当x＞0时，y随x的增大而增大判断出k﹣3的符号，求出k的取值范围即可．

【解答】解：∵反比例函数y=的图象，当x＞0时，y随x的增大而增大，

∴k﹣3＜0，解得k＜3．

故答案为：k＜3．

第36题

如图，菱形ABCD中，对角线AC与BD相交于点O，OE∥DC交BC于点E，若AD=8cm，则OE的长为　　cm．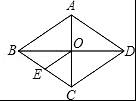

参考答案：4

解析：

【考点】菱形的性质；三角形中位线定理．

【分析】根据已知可得OE是△ABC的中位线，从而求得OE的长．

【解答】解：∵OE∥DC，AO=CO

∴OE是△ABC的中位线

∵AB=AD=8cm

∴OE=4cm．

故答案为4．

第37题

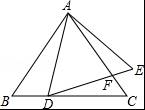
如图，已知△ABC和△ADE均为等边三角形，点D在BC边上，DE与AC相交于点F，如果AB=9，BD=3，那么CF的长度为　　．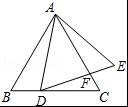

参考答案：2

解析：

【考点】相似三角形的判定与性质；等边三角形的性质．

【分析】利用两对相似三角形，线段成比例：AB：BD=AE：EF，CD：CF=AE：EF，可得CF=2．

【解答】解：如图，∵△ABC和△ADE均为等边三角形，

∴∠B=∠BAC=60°，∠E=∠EAD=60°，

∴∠B=∠E，∠BAD=∠EAF，

∴△ABD∽△AEF，

∴AB：BD=AE：EF．

同理：△CDF∽△EAF，

∴CD：CF=AE：EF，

∴AB：BD=CD：CF，

即9：3=（9﹣3）：CF，

∴CF=2．

故答案为：2．

第38题

某小区2012年屋顶绿化面积为2000平方米，计划2014年屋顶绿化面积要达到2880平方米，如果每年屋顶绿化面积的增长率相同，那么这个增长率是　　．

参考答案：20%

解析：

【考点】一元二次方程的应用．

【分析】一般用增长后的量=增长前的量×（1+增长率），如果设人均年收入的平均增长率为x，根据题意即可列出方程．

【解答】解：设平均增长率为x，根据题意可列出方程为：

2000（1+x）²=2880，

（1+x）²=1.44．

1+x=±1.2．

所以x₁=0.2，x₂=﹣2.2（舍去）．

故x=0.2=20%．

即：这个增长率为20%．

故答案是：20%．

第39题

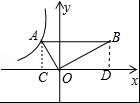
如图，Rt△ABO中，∠AOB=90°，∠ABO=30°，点A在第二象限，点B在第一象限，过点A的反比例函数表达式为y=﹣，则过点B的反比例函数表达式为　　．

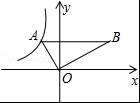
参考答案：y=3/x

解析：

【考点】待定系数法求反比例函数解析式．

【分析】解直角三角形求得=，然后过A作AC⊥x轴于点C，过B作BD⊥x轴于点D，可证明△AOC∽△OBD，由点A在y=﹣上，可求得△AOC的面积，由相似三角形的性质可求得△BOD的面积，可求得答案．

【解答】解：∵Rt△ABO中，∠AOB=90°，∠ABO=30°，

∴tan30°==，

如图，过A作AC⊥x轴，过B作BD⊥x轴，垂足分别为C、D，

∵∠AOB=90°，

∴∠BOD+∠AOC=∠DBO+∠BOD，

∴∠DBO=∠AOC，

∴△AOC∽△OBD，

∴=（）²=（）²=，

设A点坐标为（x_A，y_A），

∵点A在函数y=﹣的图象上，

∴x_Ay_A=k=﹣1，

∴S_△AOC=|k|=，

∴S_△OBD=3S_△AOC=，

设B点坐标为（x_B，y_B），

∴x_By_B=，

∴x_By_B=3，

∴过B点的反比例函数的解析式为y=，

故答案为：y=．

第40题

计算：2cos30°﹣tan45°﹣．

参考答案：见解析

解析：

【考点】特殊角的三角函数值．

【分析】直接把各特殊角的三角函数值代入进行计算即可．

【解答】解：原式=2×﹣1﹣

=﹣1﹣（﹣1）

=0．