九年级（上）期末数学试卷集（328题）

---

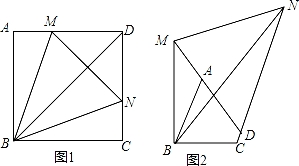
如图1，在正方形ABCD中，点M、N分别在AD、CD上．

（1）若∠MBN=45°且∠ABM=∠CBN，则易证　　　　　　．（选择正确答案填空）

①AM+CN＞MN；②（AM+CN）=MN；③MN=AM+CN．

（2）若∠MBN=∠ABC，在（1）中线段MN、AM、CN之间的数量关系是否仍然成立？若成立给予证明，若不成立探究出它们之间关系．

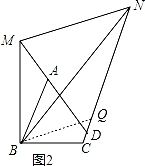
【拓展】如图2，在四边形ABCD中，AB=BC，∠ABC与∠ADC互补．点M、N分别在DA、CD的延长线上，若∠MBN=∠ABC，试探究线段MN、AM、CN又有怎样的数量关系？请写出猜想并证明．

知识点：试卷01

参考答案：见解析

解析：

【考点】四边形综合题．

【专题】综合题．

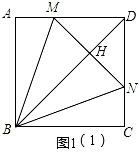
【分析】（1）设BD于MN交于点H，如图1（1），根据正方形的性质得∠ABH=∠CBH=45°，BA=BC，由于∠MBN=45°，∠ABM=∠CBN，则∠ABM=∠HBM=∠HBN=∠CBN，再证明△ABM≌△CBN得到BM=BN，AM=CN，接着根据等腰三角形的性质可判断BH⊥MN，于是根据角平分线的性质得MA=MH，NH=NC，所以有MN=AM+CN；

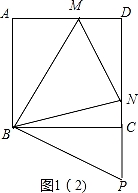
（2）把△BAM绕点B顺时针旋转90°得到△BCP，如图1（2），根据旋转的性质得BM=BP，AM=CP，∠MBP=90°，∠BCP=∠A=90°，再证明点P在DC的延长线上，则NC+CP=NP，利用∠MBN=∠ABC=45°得到∠NBP=45°，接着可证明△BNM≌△BNP，则MN=NP，于是有MN=CP+CN=AM+CN；

【拓展】如图2，由于∠ABC+∠ADC=180°，根据四边形内角和得到∠BAD+∠BCD=180°，则∠BAM=∠BCD，根据旋转的定义，可把△BAM绕点B顺时针旋转90°得到△BCQ，则根据旋转的性质得∠BAM=∠BCQ，BM=BQ，∠MBQ=∠ABC，则∠BCQ=∠BCD，则可判断点Q在CN上得到CN=CQ+MQ=AM+NQ，然后证明△BMN≌△BQN得到MN=QN，则CN=AM+MN．

【解答】（1）解：设BD于MN交于点H，如图1（1），

∵BD为正方形ABCD的正方形，

∴∠ABH=∠CBH=45°，BA=BC，

∵∠MBN=45°，∠ABM=∠CBN，

∴∠ABM=∠HBM=∠HBN=∠CBN，

在△ABM和△CBN中

，

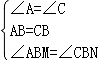∴△ABM≌△CBN，

∴BM=BN，AM=CN，

而∠HBM=∠HBN，

∴BH⊥MN，

∴MA=MH，NH=NC，

∴AM=MH=HN=NC，

∴MN=AM+CN；

故答案为③；

（2）解：在（1）中线段MN、AM、CN之间的数量关系仍然成立．理由如下：

把△BAM绕点B顺时针旋转90°得到△BCP，如图1（2），

∴BM=BP，AM=CP，∠MBP=90°，∠BCP=∠A=90°，

∵∠BCP+∠BCN=180°，

∴点P在DC的延长线上，

∴NC+CP=NP，

∵∠MBN=∠ABC=45°，

∴∠NBP=45°，

在△BNM和△BNP中

，

∴△BNM≌△BNP，

∴MN=NP，

∴MN=CP+CN=AM+CN；

【拓展】解：如图2，∵∠ABC+∠ADC=180°，

∴∠BAD+∠BCD=180°，

而∠BAD+∠BAM=180°，

∴∠BAM=∠BCD，

∵AB=BC，

∴把△BAM绕点B顺时针旋转90°得到△BCQ，

∴∠BAM=∠BCQ，BM=BQ，∠MBQ=∠ABC，

∴∠BCQ=∠BCD，

∴点Q在CN上，

∴CN=CQ+MQ=AM+NQ，

∵∠MBN=∠ABC，

∴∠MBN=MBQ，[来源:Zxxk.Com]

∴∠MBN=∠QBN，

在△BMN和△BQN中[来源:Zxxk.Com]

，

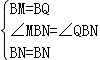∴△BMN≌△BQN，

∴MN=QN，

∴CN=AM+MN，

即MN=CN﹣AM．

 

 

 

【点评】本题考查了四边形的综合题：熟练掌握正方形的性质和旋转的性质；灵活应用全等三角形的判定与性质解决线段相等的问题；解决本题的关键是构建全等三角形．