九年级（上）期末数学试卷集（328题）

---

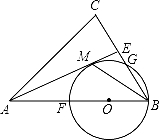
已知：如图，在△ABC中，AB=AC，AE是角平分线，BM平分∠ABC交AE于点M，经过B，M两点的⊙O交BC于点G，交AB于点F，FB恰为⊙O的直径．

（1）求证：AE与⊙O相切；

（2）当BC=4，cosC=时，求⊙O的半径．

 

知识点：试卷01

参考答案：见解析

解析：

【考点】切线的判定；等腰三角形的性质；相似三角形的判定与性质；解直角三角形．

【专题】几何综合题．

【分析】（1）连接OM，证明OM∥BE，再结合等腰三角形的性质说明AE⊥BE，进而证明OM⊥AE；

（2）结合已知求出AB，再证明△AOM∽△ABE，利用相似三角形的性质计算．

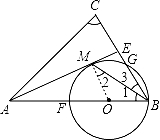
【解答】（1）证明：连接OM，则OM=OB

∴∠1=∠2

∵BM平分∠ABC

∴∠1=∠3

∴∠2=∠3

∴OM∥BC

∴∠AMO=∠AEB

在△ABC中，AB=AC，AE是角平分线

∴AE⊥BC

∴∠AEB=90°

∴∠AMO=90°

∴OM⊥AE

∵点M在圆O上，

∴AE与⊙O相切；

 

（2）解：在△ABC中，AB=AC，AE是角平分线

∴BE=BC，∠ABC=∠C

∵BC=4，cosC=

∴BE=2，cos∠ABC=

在△ABE中，∠AEB=90°

∴AB==6

设⊙O的半径为r，则AO=6﹣r

∵OM∥BC

∴△AOM∽△ABE

∴

∴

解得

∴⊙O的半径为．

 

【点评】本题是小综合题，考查等腰三角形，平行线，角平分线，直线和圆的位置关系，相似三角形等知识点．