九年级（上）期末数学试卷集（328题）

---

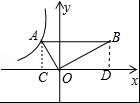
如图，Rt△ABO中，∠AOB=90°，∠ABO=30°，点A在第二象限，点B在第一象限，过点A的反比例函数表达式为y=﹣，则过点B的反比例函数表达式为　　．

知识点：试卷02

参考答案：y=3/x

解析：

【考点】待定系数法求反比例函数解析式．

【分析】解直角三角形求得=，然后过A作AC⊥x轴于点C，过B作BD⊥x轴于点D，可证明△AOC∽△OBD，由点A在y=﹣上，可求得△AOC的面积，由相似三角形的性质可求得△BOD的面积，可求得答案．

【解答】解：∵Rt△ABO中，∠AOB=90°，∠ABO=30°，

∴tan30°==，

如图，过A作AC⊥x轴，过B作BD⊥x轴，垂足分别为C、D，

∵∠AOB=90°，

∴∠BOD+∠AOC=∠DBO+∠BOD，

∴∠DBO=∠AOC，

∴△AOC∽△OBD，

∴=（）²=（）²=，

设A点坐标为（x_A，y_A），

∵点A在函数y=﹣的图象上，

∴x_Ay_A=k=﹣1，

∴S_△AOC=|k|=，

∴S_△OBD=3S_△AOC=，

设B点坐标为（x_B，y_B），

∴x_By_B=，

∴x_By_B=3，

∴过B点的反比例函数的解析式为y=，

故答案为：y=．