第61题

若关于x的一元二次方程x²﹣3x+c=0有一个根是2，则另一根是　　．

参考答案：1

解析：

【考点】根与系数的关系．

【分析】首先设另一个根为α，由关于x的一元二次方程x²﹣3x+c=0有一个根是2，根据根与系数的关系可得α+2=3，继而求得答案．

【解答】解：设另一个根为α，

∵关于x的一元二次方程x²﹣3x+c=0有一个根是2，

∴α+2=3，

∴α=1，

即另一个根为1．

故答案为1．

第62题

如果方程x²+2x+m=0有两个同号的实数根，m的取值范围是　　

参考答案：0＜m≤1

解析：

【考点】根的判别式；根与系数的关系．

【分析】根据题意得出△≥0，m＞0，代入求出m的范围即可．

【解答】解：∵方程x²+2x+m=0有两个同号的实数根，

∴△≥0，m＞0，

△=2²﹣4×1×m=4﹣4m≥0，

解得：m≤1，

即m的取值范围是0＜m≤1，

故答案为：0＜m≤1．

第63题

已知线段a=3cm，b=6cm，c=5cm，且a，b，d，c成比例线段，则d=　　cm．

参考答案：2.5

解析：

【考点】比例线段．

【分析】根据线段成比例，则可以列出方程a：b=d：c，代入数值求解即可．

【解答】解：∵线段a，b，c，d成比例，

∴a：b=d：c，

由题中a=3cm，b=6cm，c=5cm，

∴代入方程可得d=2.5．

第64题

如图，把△ABC沿AB边平移到△A′B′C′的位置，它们的重叠部分（即图中的阴影部分）的面积是△ABC的面积的一半，若AB=，则此三角形移动的距离AA′=　　．

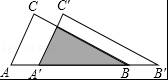
参考答案：√（2）-1

解析：

【考点】相似三角形的判定与性质；平移的性质．

【分析】利用相似三角形面积的比等于相似比的平方先求出A′B，再求AA′就可以了．

【解答】解：设BC与A′C′交于点E，

由平移的性质知，AC∥A′C′，

∴△BEA′∽△BCA，

∴S_△BEA′：S_△BCA=A′B²：AB²=1：2，

∵AB=，

∴A′B=1，

∴AA′=AB﹣A′B=，

故答案为：．

第65题

学校校园内有一块如图所示的三角形空地，计划将这块空地建成一个花园，以美化校园环境．预计花园每平方米造价为30元，学校建这个花园需要投资　　元．（精确到1元）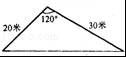

参考答案：7794

解析：

【考点】解直角三角形的应用．

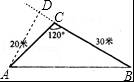
【分析】延长BC，过A作AD⊥BC的延长线于点D，再根据补角的定义求出∠ACD的度数，由锐角三角函数的定义接可求出AD的长，再根据三角形的面积公式求出此三角形的面积，再根据每平方米造价为30元计算出所需投资即可．

【解答】解：延长BC，过A作AD⊥BC的延长线于点D，

∵∠ACB=120°，

∴∠ACD=180°﹣120°=60°，

∵AC=20米，

∴AD=AC•sin60°=20×=10（米），

∴S_△ABC=BC•AD=×30×10=150（平方米），

∴所需投资=150×30≈7794（元）．

故答案为：7794．

第66题

如图，条形统计图是从曙光中学800名学生中帮助失学儿童捐款金额的部分抽样调查数据，扇形图统计图是该校各年级人数比例分布图．那么该校七年级同学捐款的总数大约为　　元．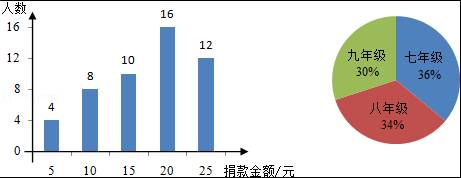

参考答案：5010

解析：

【考点】条形统计图；扇形统计图．

【分析】首先根据扇形统计图和已知条件求出七年级同学的人数，然后求出样本平均数，再利用样本估计总体的思想即可求出该校七年级同学捐款的总数．

【解答】解：∵曙光中学有800名学生，

∴七年级同学的人数为：800×36%=288人，

而抽样调查数据平均数为： =≈17.4元，

∴17.4×288≈5010元，

∴该校七年级同学捐款的总数为5010元，

故答案为：5010．

第67题

用适当的方法解下列方程：

（1）4（x﹣3）²﹣25=0

参考答案：见解析

解析：

【考点】解一元二次方程-因式分解法；解一元二次方程-直接开平方法．

【分析】（1）先移项得到4（x﹣3）²=25，然后利用直接开平方法解方程；

（2）利用因式分解法解方程．

【解答】解：（1）4（x﹣3）²=25，

2（x﹣3）=±5，

所以x₁=，x₂=；

（2）（2x﹣1）（x+4）=0，

2x﹣1=0或x+4=0，

所以x₁=，x₂=﹣4．

第68题

已知反比例函数y=（k为常数，k≠1）．

（1）若点A（1，2）在这个函数的图象上，求k的值；

参考答案：见解析

解析：

【考点】反比例函数图象上点的坐标特征；反比例函数的性质．

【分析】（1）根据反比例函数图象上点的坐标特征得到k﹣1=1×2，然后解方程即可；

（2）根据反比例函数的性质得k﹣1＞0，然后解不等式即可．

【解答】解：（1）根据题意得k﹣1=1×2，

解得k=3；

（2）因为反比例函数y=，在这个函数图象的每一分支上，y随x的增大而减小，

所以k﹣1＞0，

解得k＞1．

第69题

计算下列各题：

（1）tan45°﹣sin60°•cos30°；

参考答案：见解析

解析：

【考点】实数的运算；特殊角的三角函数值．

【分析】（1）原式利用特殊角的三角函数值计算即可得到结果；

（2）原式利用特殊角的三角函数值计算即可得到结果．

【解答】解：（1）原式=1﹣×=1﹣=；

（2）原式=×+×=．

第70题

关于x的一元二次方程x²﹣3x﹣k=0有两个不相等的实数根．

（1）求k的取值范围；

参考答案：见解析

解析：

【考点】根的判别式；解一元二次方程-公式法．

【分析】（1）因为方程有两个不相等的实数根，△＞0，由此可求k的取值范围；

（2）在k的取值范围内，取负整数，代入方程，解方程即可．

【解答】解：（1）∵方程有两个不相等的实数根，

∴（﹣3）²﹣4（﹣k）＞0，

即4k＞﹣9，解得；

（2）若k是负整数，k只能为﹣1或﹣2；

如果k=﹣1，原方程为x²﹣3x+1=0，

解得，，．

（如果k=﹣2，原方程为x²﹣3x+2=0，解得，x₁=1，x₂=2）

第71题

如图，在△ABC中，DE∥BC，EF∥AB，求证：△ADE∽△EFC．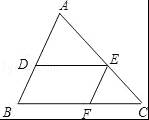

参考答案：见解析

解析：

【考点】相似三角形的判定；平行线的性质．

【分析】根据平行线的性质可知∠AED=∠C，∠A=∠FEC，根据相似三角形的判定定理可知△ADE∽△EFC．

【解答】证明：∵DE∥BC，

∴∠AED=∠C．

又∵EF∥AB，

∴∠A=∠FEC．

∴△ADE∽△EFC．

第72题

如图，路灯（P点）距地面8米，身高1.6米的小明从距路灯的底部（O点）20米的A点，沿OA所在的直线行走14米到B点时，身影的长度是变长了还是变短了？变长或变短了多少米？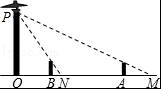

参考答案：见解析

解析：

【考点】相似三角形的应用．

【分析】如图，由于AC∥BD∥OP，故有△MAC∽△MOP，△NBD∽△NOP即可由相似三角形的性质求解．

【解答】解：∵∠MAC=∠MOP=90°，

∠AMC=∠OMP，

∴△MAC∽△MOP．

∴，

即，

解得，MA=5米；

同理，由△NBD∽△NOP，可求得NB=1.5米，

∴小明的身影变短了5﹣1.5=3.5米．

第73题

马航MH370失联后，我国政府积极参与搜救．某日，我两艘专业救助船A、B同时收到有关可疑漂浮物的讯息，可疑漂浮物P在救助船A的北偏东53.50°方向上，在救助船B的西北方向上，船B在船A正东方向140海里处．（参考数据：sin36.5°≈0.6，cos36.5°≈0.8，tan36.5°≈0.75）．

（1）求可疑漂浮物P到A、B两船所在直线的距离；

参考答案：见解析

解析：

【考点】解直角三角形的应用-方向角问题．

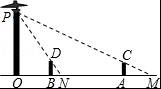
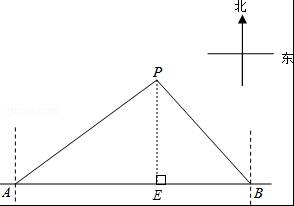
【分析】（1）过点P作PE⊥AB于点E，在Rt△APE中解出PE即可；

（2）分别求出PA、PB的长，根据两船航行速度，计算出两艘船到达P点时各自所需要的时间，即可作出判断．

【解答】解：（1）过点P作PE⊥AB于点E，

由题意得，∠PAE=36.5°，∠PBA=45°，

设PE为x海里，则BE=PE=x海里，

∵AB=140海里，

∴AE=海里，

在Rt△PAE中，，

即：

解得：x=60，

∴可疑漂浮物P到A、B两船所在直线的距离约为60海里；

（2）在Rt△PBE中，PE=60海里，∠PBE=45°，

则BP=PE=60≈84.8海里，

B船需要的时间为：84.8÷30≈2.83小时，

在Rt△PAE中， =sin∠PAE，

∴AP=PE÷sin∠PAE=60÷0.6=100海里，

∴A船需要的时间为：100÷40=2.5小时，

∵2.83＞2.5，

∴A船先到达．

第74题

如图，已知反比例函数y=（x＞0，k是常数）的图象经过点A（1，4），点B（m，n），其中m＞1，AM⊥x轴，垂足为M，BN⊥y轴，垂足为N，AM与BN的交点为C．

（1）写出反比例函数解析式；

参考答案：见解析

解析：

【考点】反比例函数综合题．

【分析】（1）把A点坐标代入y=可得k的值，进而得到函数解析式；

（2）根据A、B两点坐标可得AC=4﹣n，BC=m﹣1，ON=n，OM=1，则=，再根据反比例函数解析式可得=n，则=m﹣1，而=，可得=，再由∠ACB=∠NOM=90°，可得△ACB∽△NOM；

（3）根据△ACB与△NOM的相似比为2可得m﹣1=2，进而得到m的值，然后可得B点坐标，再利用待定系数法求出AB的解析式即可．

【解答】解：（1）∵y=（x＞0，k是常数）的图象经过点A（1，4），

∴k=4，

∴反比例函数解析式为y=；

（2）∵点A（1，4），点B（m，n），

∴AC=4﹣n，BC=m﹣1，ON=n，OM=1，

∴==﹣1，

∵B（m，n）在y=上，

∴=n，

∴=m﹣1，而=，

∴=，

∵∠ACB=∠NOM=90°，

∴△ACB∽△NOM；

（3）∵△ACB与△NOM的相似比为2，

∴m﹣1=2，

m=3，

∴B（3，），

设AB所在直线解析式为y=kx+b，

∴，

解得，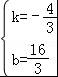

∴解析式为y=﹣x+．

第75题

﹣7的倒数是（　　）

A.7

B.﹣7

C.

D.﹣

参考答案：D

解析：

【考点】倒数．

【分析】根据乘积是1的两个数互为倒数，可得一个数的倒数．

【解答】解：﹣7的倒数是﹣，

故选：D．

【点评】本题考查了倒数，分子分母交换位置是求一个数的倒数的关键．

第76题

现在网购越来越多地成为人们的一种消费方式，在2014年的“双11”网上促销活动中天猫和淘宝的支付交易额突破57000 000 000元，将数字57000 000 000用科学记数法表示为（　　）

A.5.7×10⁹

B.5.7×10¹⁰

C.0.57×10¹¹

D.57×10⁹

参考答案：B

解析：

【考点】科学记数法—表示较大的数．

【分析】科学记数法的表示形式为a×10ⁿ的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．

【解答】解：将57000000000用科学记数法表示为：5.7×10¹⁰．

故选：B．

【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10ⁿ的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．

第77题

如图所示的几何体是由一个圆柱体和一个长方形组成的，则这个几何体的俯视图是（　　）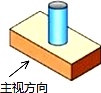

A.

B.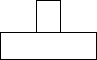

C.

D.

参考答案：C

解析：

【考点】简单组合体的三视图．

【专题】常规题型．

【分析】根据俯视图是从上面看得到的图形，可得答案．

【解答】解：从上面看外边是一个矩形，里面是一个圆，

故选：C．

【点评】本题考查了简单组合体的三视图，俯视图是从上面看得到的图形．

第78题

下列计算正确的是（　　）

A.a²+a²=a⁴

B.2a﹣a=2

C.（ab）²=a²b²

D.（a²）³=a⁵

参考答案：C

解析：

【考点】幂的乘方与积的乘方；合并同类项．

【分析】根据合并同类项的法则，同底数幂的乘法以及幂的乘方的知识求解即可求得答案．

【解答】解：A、a²+a²=2a²，故本选项错误；

B、2a﹣a=a，故本选项错误；

C、（ab）²=a²b²，故本选项正确；

D、（a²）³=a⁶，故本选项错误；

故选：C．

【点评】本题考查了同底数幂的乘法，合并同类项，一定要记准法则才能做题．

第79题

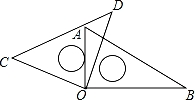
将一副直角三角尺如图放置，若∠AOD=20°，则∠BOC的大小为（　　）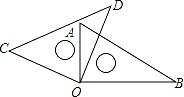

A.140°

B.160°

C.170°

D.150°

参考答案：B

解析：

【考点】直角三角形的性质．

【分析】利用直角三角形的性质以及互余的关系，进而得出∠COA的度数，即可得出答案．

【解答】解：∵将一副直角三角尺如图放置，∠AOD=20°，

∴∠COA=90°﹣20°=70°，

∴∠BOC=90°+70°=160°．

故选：B．

【点评】此题主要考查了直角三角形的性质，得出∠COA的度数是解题关键．

第80题

一只不透明的袋子中装有4个黑球、2个白球，每个球除颜色外都相同，从中任意摸出3个球，下列事件为必然事件的是（　　）

A.至少有1个球是黑球

B.至少有1个球是白球

C.至少有2个球是黑球

D.至少有2个球是白球

参考答案：A

解析：

【考点】随机事件．

【分析】由于只有2个白球，则从中任意摸出3个球中至少有1个球是黑球，于是根据必然事件的定义可判断A选项正确．

【解答】解：一只不透明的袋子中装有4个黑球、2个白球，每个球除颜色外都相同，从中任意摸出3个球，至少有1个球是黑球是必然事件；至少有1个球是白球、至少有2个球是黑球和至少有2个球是白球都是随机事件．

故选A．

【点评】本题考查了随机事件：在一定条件下，可能发生也可能不发生的事件，称为随机事件．事件分为确定事件和不确定事件（随机事件），确定事件又分为必然事件和不可能事件