九年级（上）期末数学试卷集（328题）

---

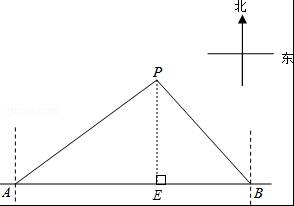
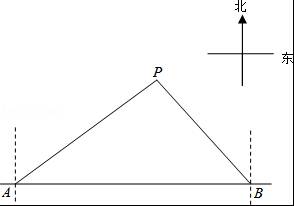
马航MH370失联后，我国政府积极参与搜救．某日，我两艘专业救助船A、B同时收到有关可疑漂浮物的讯息，可疑漂浮物P在救助船A的北偏东53.50°方向上，在救助船B的西北方向上，船B在船A正东方向140海里处．（参考数据：sin36.5°≈0.6，cos36.5°≈0.8，tan36.5°≈0.75）．

（1）求可疑漂浮物P到A、B两船所在直线的距离；

（2）若救助船A、救助船B分别以40海里/时，30海里/时的速度同时出发，匀速直线前往搜救，试通过计算判断哪艘船先到达P处．

知识点：试卷03

参考答案：见解析

解析：

【考点】解直角三角形的应用-方向角问题．

【分析】（1）过点P作PE⊥AB于点E，在Rt△APE中解出PE即可；

（2）分别求出PA、PB的长，根据两船航行速度，计算出两艘船到达P点时各自所需要的时间，即可作出判断．

【解答】解：（1）过点P作PE⊥AB于点E，

由题意得，∠PAE=36.5°，∠PBA=45°，

设PE为x海里，则BE=PE=x海里，

∵AB=140海里，

∴AE=海里，

在Rt△PAE中，，

即：

解得：x=60，

∴可疑漂浮物P到A、B两船所在直线的距离约为60海里；

 

（2）在Rt△PBE中，PE=60海里，∠PBE=45°，

则BP=PE=60≈84.8海里，

B船需要的时间为：84.8÷30≈2.83小时，

在Rt△PAE中， =sin∠PAE，

∴AP=PE÷sin∠PAE=60÷0.6=100海里，

∴A船需要的时间为：100÷40=2.5小时，

∵2.83＞2.5，

∴A船先到达．