九年级（上）期末数学试卷集（328题）

---

三角形两边的长分别是8和6，第三边的长是一元二次方程x²﹣16x+60=0的一个实数根，则该三角形的面积是（　　）

A.24

B.24或8

C.48或16

D.8

知识点：试卷03

参考答案：B

解析：

【考点】解一元二次方程-因式分解法；勾股定理；勾股定理的逆定理．

【分析】由x²﹣16x+60=0，可利用因式分解法求得x的值，然后分别从x=6时，是等腰三角形；与x=10时，是直角三角形去分析求解即可求得答案．

【解答】解：∵x²﹣16x+60=0，

∴（x﹣6）（x﹣10）=0，

解得：x₁=6，x₂=10，

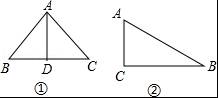
当x=6时，则三角形是等腰三角形，如图①，AB=AC=6，BC=8，AD是高，

∴BD=4，AD==2，

∴S_△ABC=BC•AD=×8×2=8；

当x=10时，如图②，AC=6，BC=8，AB=10，

∵AC²+BC²=AB²，

∴△ABC是直角三角形，∠C=90°，

S_△ABC=BC•AC=×8×6=24．

∴该三角形的面积是：24或8．

故选：B．