九年级（上）期末数学试卷集（328题）

---

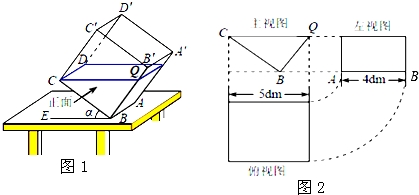
一透明的敞口正方体容器ABCD﹣A′B′C′D′装有一些液体，棱AB始终在水平桌面上，容器底部的倾斜角为α （∠CBE=α，如图所示）．

探究 如图1，液面刚好过棱CD，并与棱BB′交于点Q，此时液体的形状为直三棱柱，其三视图及尺寸如图2所示．解决问题：

（1）CQ与BE的位置关系是　　，BQ的长是　　dm；

（2）求液体的体积；（参考算法：直棱柱体积V液=底面积S_△BCQ×高AB）；

（3）求液面到桌面的高度和倾斜角α的度数．（注：sin37°=，tan37°=）．

知识点：试卷01

参考答案：见解析

解析：

【考点】解直角三角形的应用．

【分析】（1）根据水面与水平面平行可以得到CQ与BE平行，利用勾股定理即可求得BQ的长；

（2）液体正好是一个以△BCQ是底面的直棱柱，据此即可求得液体的体积；

（3）求出∠BCQ的正切值即可得到其度数．

【解答】解：（1）CQ∥BE，BQ==3dm；

故答案为：平行，3；

 

（2）V_液=×3×4×4=24（dm³）；

 

（3）过点B作BF⊥CQ，垂足为F，

∵×3×4=×5×BF，

∴BF=，

∴液面到桌面的高度；

∵在Rt△BCQ中，tan∠BCQ=，

∴α=∠BCQ=37°．

 

【点评】本题考查了解直角三角形的应用，熟练掌握四边形的体积计算以及对三视图的认识，正确理解棱柱的体积的计算是关键．