九年级（上）期末数学试卷集（328题）

---

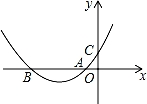
如图为抛物线y=ax²+bx+c的图象，A、B、C 为抛物线与坐标轴的交点，且OA=OC=1，则下列关系中正确的是（　　）

A.ac＜0

B.a﹣b=1

C.a+b=﹣1

D.b＞2a

知识点：试卷01

参考答案：D

解析：

【考点】二次函数图象与系数的关系．

【分析】根据以下知识点分析即可：①二次项系数a决定抛物线的开口方向和大小：当a＞0时，抛物线向上开口；当a＜0时，抛物线向下开口；②一次项系数b和二次项系数a共同决定对称轴的位置：当a与b同号时（即ab＞0），对称轴在y轴左； 当a与b异号时（即ab＜0），对称轴在y轴右．（简称：左同右异）③常数项c决定抛物线与y轴交点． 抛物线与y轴交于（0，c）．

【解答】解：∵OC=1，

∴c=1，

又∵x=1时，y＞0，

∴a+b+1＞0，

∴a+b＞﹣1，

∴选项A不正确；

 

∵抛物线开口向上，

∴a＞0；

又∵c=1，

∴ac=a＞0，

∴选项B不正确；

 

∵OA=1，[来源:学科网ZXXK]

∴x=﹣＜﹣1，

又∵a＞0，

∴b＞2a，

∴选项C不正确；

 

∵OA=1，

∴x=﹣1时，y=0，

∴a﹣b+c=0，

又∵c=1，

∴a﹣b=﹣1，

∴选项D正确．

故选：D．

【点评】此题主要考查了二次函数的图象与系数的关系，要熟练掌握，解答此题的关键是要明确二次函数各项的系数和图形的关系．