九年级（上）期末数学试卷集（328题）

---

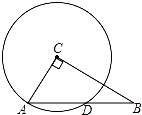
如图，在直角三角形ABC中，∠ACB=90°，AC=1，BC=2，以点C为圆心，CA为半径的圆与AB交于点D，则AD的长为　　．

知识点：试卷01

参考答案：

解析：

【考点】垂径定理；勾股定理．

【分析】作CE⊥AB于E，根据勾股定理得到AB=，利用三角形面积公式求出CE，根据勾股定理求出AE，根据垂径定理计算即可．

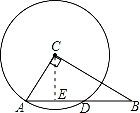
【解答】解：作CE⊥AB于E，

则AE=AD，

∵∠ACB=90°，AC=1，BC=2，

∴AB==，

×AB×CE=AC×BC，即×CE=，

解得，CE=，

AE==，

则AD=2AE=，

故答案为：．

 

【点评】本题考查的是勾股定理和垂径定理的应用，垂径定理：垂直弦的直径平分这条弦，并且平分弦所对的两条弧．