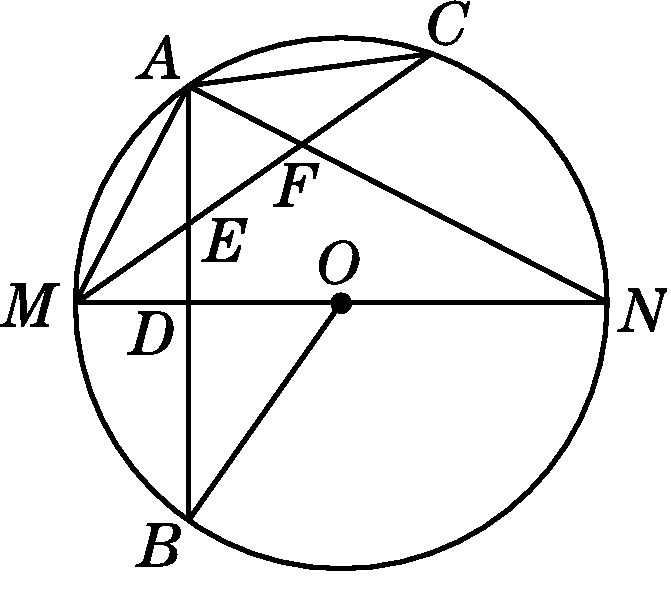第181题

如图，△ABC内接于⊙O，CD是⊙O的直径，∠BCD＝54°，则∠A的度数是(　　)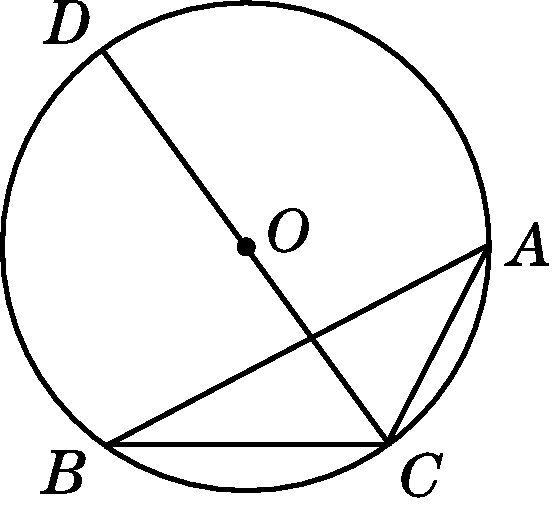

A.36°

B.33°

C.30°

D.27°

参考答案：A

解析：

点拨：连接BD，∵CD是⊙O的直径，∴∠DBC＝90°，∴∠BDC＝90°－∠BCD＝90°－54°＝36°，∴∠A＝∠BDC＝36°.

第182题

一个盒子内装有大小、形状相同的四个球，其中红球1个、绿球1个、白球2个，小明摸出一个球不放回，再摸出一个球，则两次都摸到白球的概率是(　　)

)

A.

B.

C.  

D.)

参考答案：C

第183题

如图，正方形OABC绕着点O逆时针旋转40°得到正方形ODEF，连接AF，则∠OFA的度数是(　　)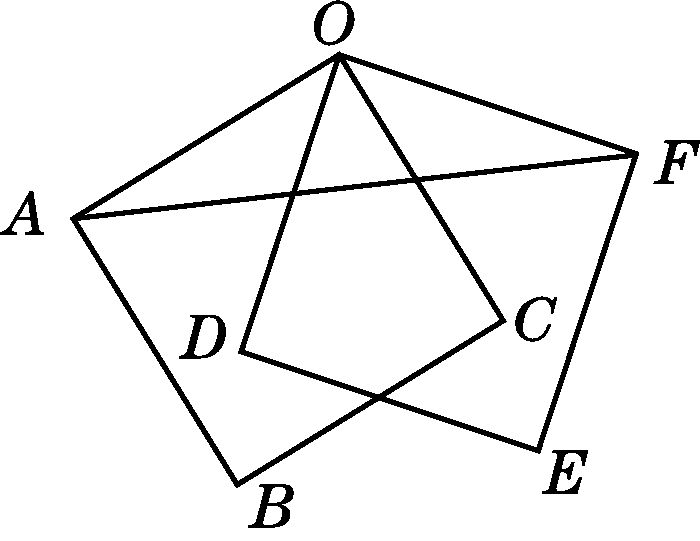

A.15°

B.20°

C.25°

D.30°

参考答案：C

解析：

点拨：∵正方形ODEF是由正方形OABC绕点O逆时针旋转40°得到的，∴∠AOC＝90°，∠COF＝40°，OA＝OF，∴∠AOF＝90°＋40°＝130°，∴∠OFA＝2(180°－130°)＝25°.

第184题

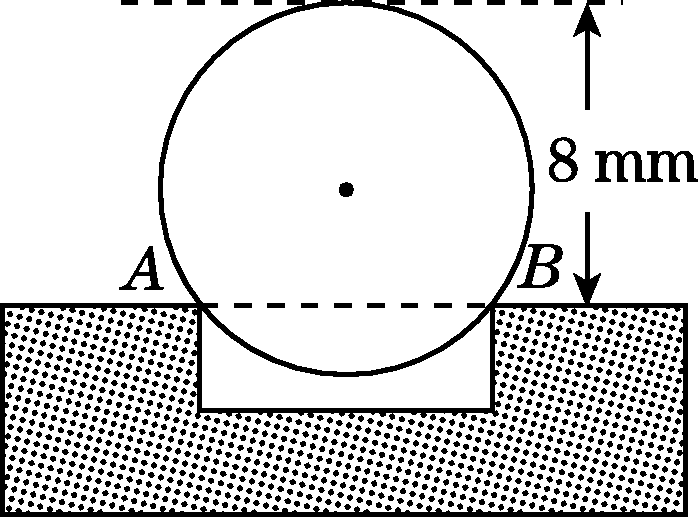
如图，在等腰直角三角形ABC中，AB＝AC＝4，点O为BC的中点，以O为圆心作半圆O交BC于点M，N，半圆O与AB，AC相切，切点分别为D，E，则半圆O的半径和∠MND的度数分别为(　　)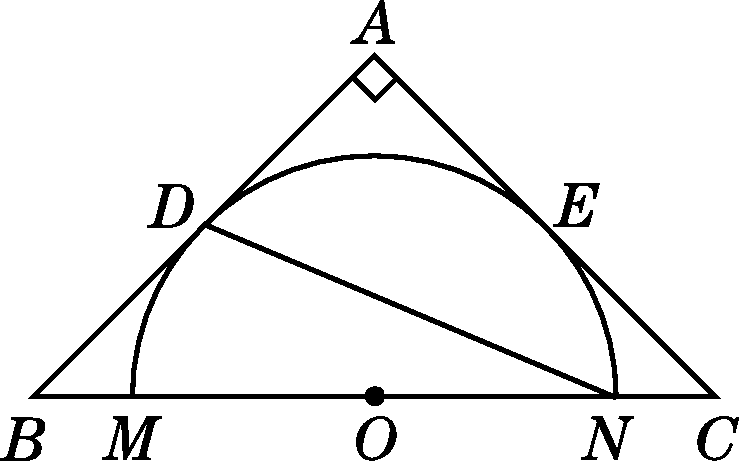

A.2，22.5°

B.3，30°

C.3，22.5°

D.2，30°

参考答案：A

第185题

如图所示，MN是⊙O的直径，作AB⊥MN，垂足为点D，连接AM，AN，点C为AN(︵)上一点，且AC(︵)＝AM(︵)，连接CM，交AB于点E，交AN于点F，现给出以下结论：

①AD＝BD；②∠MAN＝90°；③AM(︵)＝BM(︵)；④∠ACM＋∠ANM＝∠MOB；⑤AE＝MF.

A.2

B.3

C.4

D.5

参考答案：D

第186题

已知二次函数y＝ax²＋bx＋c＋2的图象如图所示，顶点为(－1，0)，下列结论：①abc＜0；②b²－4ac＝0；③a＞2；④4a－2b＋c＞0.其中正确结论的个数是(　　)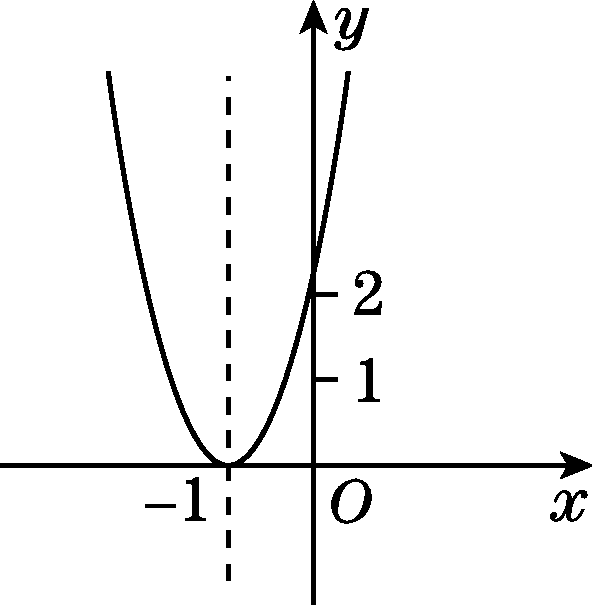

A.1

B.2

C.3

D.4

参考答案：B

解析：

点拨：∵函数图象开口向上，∴a＞0.又∵顶点为(－1，0)，∴－＝－1，∴b＝2a＞0.由抛物线与y轴的交点坐标可知：c＋2＞2，∴c＞0，∴abc＞0，故①错误．∵抛物线顶点在x轴上，∴b²－4a(c＋2)＝0.又a＞0，故②错误．∵顶点为(－1，0)，∴a－b＋c＋2＝0.∵b＝2a，∴a＝c＋2.∵c＞0，∴a＞2，故③正确．由抛物线的对称性可知x＝－2与x＝0时的函数值相等，∴4a－2b＋c＋2＞2.∴4a－2b＋c＞0，故④正确．

第187题

若关于x的一元二次方程(m－1)x²＋5x＋m²－1＝0的一个根是0，则m的值是________．

参考答案：－1

第188题

在平面直角坐标系中，点(－3，2)关于原点对称的点的坐标是________．

参考答案：(3，－2)

第189题

已知关于x的一元二次方程x²＋2x＋m＝0有实数根，则m的取值范围是________．

参考答案：m≤1

第190题

已知点A(4，y₁)，B(√2，y₂)，C(－2，y₃)都在二次函数y＝(x－2)²－1的图象上，则y₁，y₂，y₃的大小关系是________．

参考答案：y₃>y₁>y₂

第191题

工程上常用钢珠来测量零件上小孔的宽口，假设钢珠的直径是10 mm，测得钢珠顶端离零件表面的距离为8 mm，如图所示，则这个小孔的宽口AB的长度为________mm.

参考答案：8

第192题

某市组织的“五城联创”演讲比赛中，小明等25人进入总决赛，赛制规定，13人上午参赛，12人下午参赛，小明抽到上午比赛的概率是________．

参考答案：13/25

第193题

如图，在Rt△ABC中，∠ACB＝90°，AC＝4，BC＝2.分别以AC，BC为直径画半圆，则图中阴影部分的面积为________．(结果保留π)

参考答案：（5π/2）-4

解析：

第194题

如图，用一个圆心角为120°的扇形围成一个无底的圆锥，如果这个圆锥底面圆的半径为1 cm，则这个扇形的半径是________cm.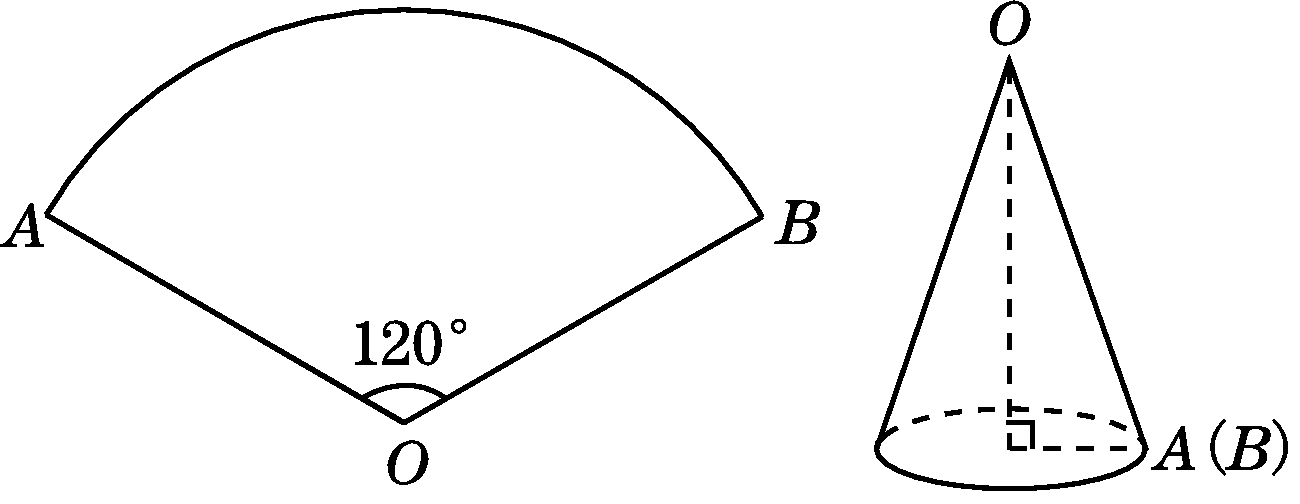

参考答案：3

解析：

点拨：扇形的弧长等于圆锥底面圆的周长，设扇形的半径为r cm，则180(120)×πr＝2π×1，解得r＝3.

第195题

如图所示，Rt△ABC的内切圆⊙O与两直角边AB，BC分别相切于点D，E，过劣弧DE(不包括端点D，E)上任一点P作⊙O的切线MN与AB，BC分别交于点M，N，若⊙O的半径为r，则Rt△MBN的周长为________．

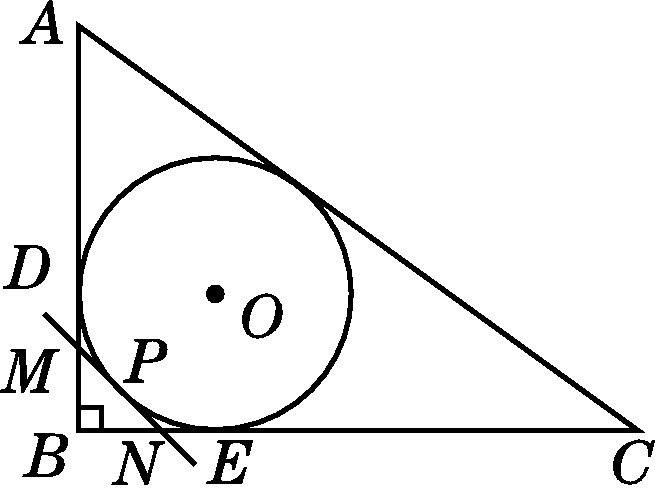
参考答案：2r

解析：

连接OD，OE.易知：BD＝BE＝r.∵MN与⊙O相切于点P，且⊙O是△ABC的内切圆，∴MD＝MP，NP＝NE.∴△MBN的周长＝BM＋MP＋PN＋BN＝BM＋MD＋NE＋BN＝BD＋BE＝2r.

第196题

如图，菱形ABCD的三个顶点在二次函数y＝ax²－2ax＋2(3)(a＜0)的图象上，点A，B分别是该抛物线的顶点和抛物线与y轴的交点，则点D的坐标为________．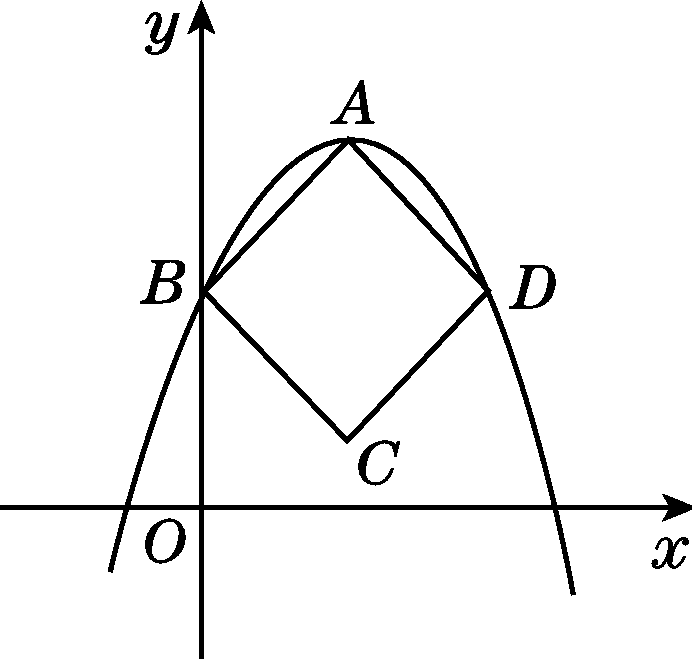

参考答案：

解析：

点拨：易知抛物线y＝ax²－2ax＋2(3)(a＜0)的对称轴是直线x＝1，与y轴的交点坐标是，∴点B的坐标是.∵菱形ABCD的三个顶点在二次函数y＝ax²－2ax＋2(3)(a＜0)的图象上，点A，B分别是抛物线的顶点和抛物线与y轴的交点，∴点B与点D关于直线x＝1对称，∴点D的坐标为)

第197题

解下列方程：

(1)2x²－4x－1＝0(配方法)；

参考答案：见解析

解析：

解：(1)由题可得，x²－2x＝2(1)，∴x²－2x＋1＝2(3).

∴(x－1)²＝2(3).

∴x－1＝

∴x₁＝

(2)由题可得，(x＋1)²－6(x＋1)＝0，∴(x＋1)(x＋1－6)＝0.

∴x＋1＝0或x＋1－6＝0.

∴x₁＝－1，x₂＝5.

第198题

已知关于x的方程x²＋ax＋a－2＝0.

(1)若该方程的一个根为1，求a的值及该方程的另一个根；

参考答案：见解析

解析：

(1)解：将x＝1代入方程x²＋ax＋a－2＝0，得1＋a＋a－2＝0.解得a＝2(1).

∴方程为x²＋2(1)x－2(3)＝0，即2x²＋x－3＝0.解得x₁＝1，x₂＝－2(3).

故a的值为2(1)，该方程的另一个根为－2(3).

(2)证明：∵Δ＝a²－4(a－2)＝a²－4a＋8＝a²－4a＋4＋4＝(a－2)²＋4>0，

∴不论a取何实数，该方程都有两个不相等的实数根．

第199题

如图，△ABC三个顶点的坐标分别为A(2，4)，B(1，1)，C(4，3)．

(1)请画出△ABC关于x轴对称的△A₁B₁C₁，并写出点A₁的坐标；[来源:学*科*网]

参考答案：见解析

解析：

解：(1)如图．点A₁的坐标为(2，－4)．

(2)如图．

(3)BC＝，所以C 点旋转到C₂点所经过的路径长＝

第200题

如图，△ABC是等腰三角形，且AC＝BC，∠ACB＝120°，在AB上取一点O，使OB＝OC，以点O为圆心，OB为半径作圆，过点C作CD∥AB交⊙O于点D，连接BD.

(1)猜想AC与⊙O的位置关系，并证明你的猜想；[来源:学,科,网Z,X,X,K]

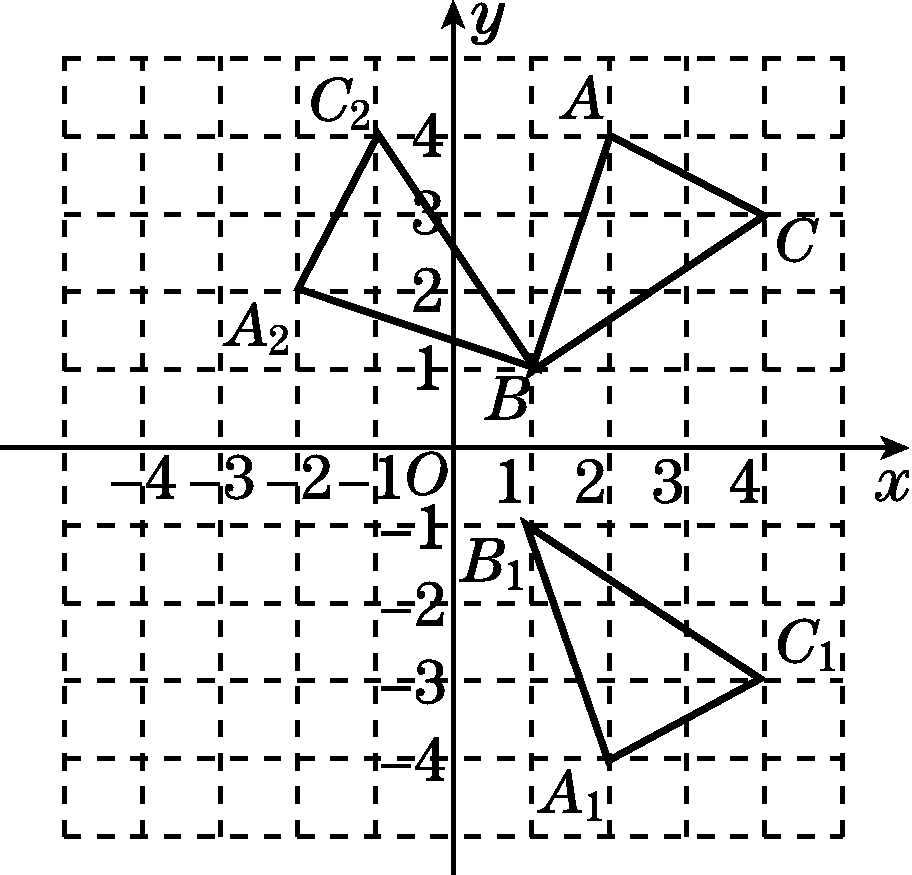
参考答案：见解析

解析：

解：(1)猜想：AC与⊙O相切．证明如下：∵AC＝BC，∠ACB＝120°，

∴∠A＝∠ABC＝30°.

∵OB＝OC，

∴∠OCB＝∠OBC＝30°.

∴∠ACO＝∠ACB－∠OCB＝90°.

∴OC⊥AC.又OC是⊙O的半径，

∴AC是⊙O的切线．

(2)四边形BOCD为菱形．证明如下：

连接OD，∵CD∥AB，

∴∠AOC＝∠OCD.

∵∠AOC＝∠OBC＋∠OCB＝60°，

∴∠OCD＝60°.[来源:学科网ZXXK]

又OC＝OD，

∴△OCD为等边三角形．

∴CD＝OD＝OB.

∴四边形BOCD为平行四边形．

又OB＝OC，∴▱BOCD为菱形．

(3)在Rt△AOC中，AC＝6，∠A＝30°，　

∴OA＝2OC.

∴OC²＋6²＝(2OC)².

解得OC＝2√3(负值舍去)．

由(2)得∠AOC＝60°，

∴∠COB＝120°.

根据扇形的弧长等于底面圆的周长，得＝2πr.解得r＝