九年级（上）期末数学试卷集（328题）

---

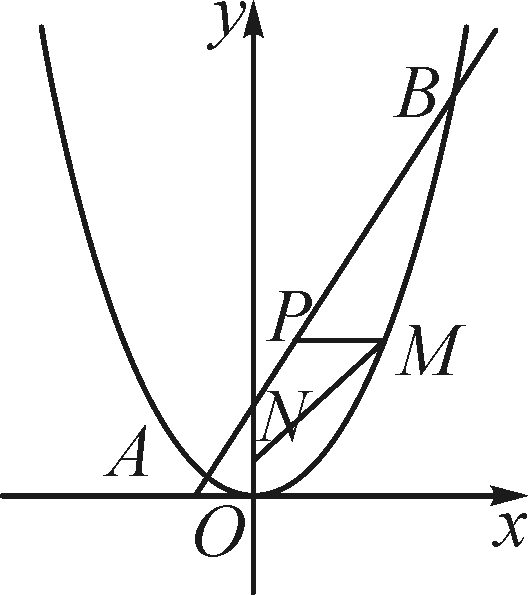
(12分)如图，已知一条直线过点(0，4)，且与抛物线y＝4(1)x²交于A，B两点，其中点A的横坐标是－2.

(1)求这条直线的解析式及点B的坐标；

(2)在x轴上是否存在点C，使得△ABC是直角三角形？若存在，求出点C的坐标，若不存在，请说明理由；

(3)过线段AB上一点P，作PM∥x轴，交抛物线于点M，点M在第一象限，点N(0，1)，当点M的横坐标为何值时，MN＋3MP的长度最大？最大值是多少？

知识点：试卷07

参考答案：见解析

解析：

解：(1)y＝2(3)x＋4，B(8，16)

(2)存在．过点B作BG∥x轴，过点A作AG∥y轴，交点为G，∴AG2＋BG2＝AB2，∵由A(－2，1)，B(8，16)可求得AB2＝325.设点C(m，0)，同理可得AC2＝(m＋2)2＋12＝m2＋4m＋5，BC2＝(m－8)2＋162＝m2－16m＋320，①若∠BAC＝90°，则AB2＋AC2＝BC2，即325＋m2＋4m＋5＝m2－16m＋320，解得m＝－2(1)；②若∠ACB＝90°，则AB2＝AC2＋BC2，即325＝m2＋4m＋5＋m2－16m＋320，解得m＝0或m＝6；③若∠ABC＝90°，则AB2＋BC2＝AC2，即m2＋4m＋5＝m2－16m＋320＋325，解得m＝32，∴点C的坐标为(－2(1)，0)，(0，0)，(6，0)，(32，0)

(3)设M(a，4(1)a2)，设MP与y轴交于点Q，在Rt△MQN中，

由勾股定理得MN＝＝4(1)a2＋1，

又∵点P与点M纵坐标相同，

∴2(3)x＋4＝4(1)a2，

∴x＝6(a2－16)，

∴点P的横坐标为6(a2－16)，

∴MP＝a－6(a2－16)，

∴MN＋3MP＝4(1)a2＋1＋3(a－6(a2－16))＝－4(1)a2＋3a＋9＝－14(a－6)2＋18，

∵－2≤6≤8，

∴当a＝6时，取最大值18，

∴当M的横坐标为6时，MN＋3MP的长度的最大值是18