“微信扫一扫”进入题库练习及模拟考试
九年级（上）期末数学试卷集（328题）
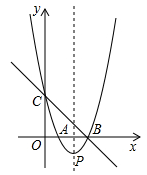
如图，直线y=-x+3与x轴、y轴分别交于点
B、点C，经过B、C两点的抛物线y=x2+bx+c与x轴的另一个交点为A，顶点为P．
（1）求该抛物线的解析式；
（2）连接AC，在x轴上是否存在点Q，使以P、B、Q为顶点的三角形与△ABC相似？若存在，请求出点Q的坐标；若不存在，请说明理由．
知识点：试卷11
参考答案：见解析
解析：
解：（1）（6分）由已知，得B（3，0），C（0，3），..............2分
∴
，..................................................................4分
解得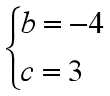
，..........................................................................5分
∴抛物线解析式为y=x2-4x+3；....................................................6分
（2）由（1），得A（1，0），连接BP，................................1分
∵∠CBA=∠ABP=45°，
∴当
时，△ABC∽△PBQ，
∴BQ=3，∴Q1（0，0），.........................................................3分
∴当
时，△ABC∽△QBP，
∴BQ=
，∴Q2（
，0）；..................................................5分
∴Q点的坐标是（0，0）或（，0）．..............................6分