九年级（上）期末数学试卷集（328题）

---

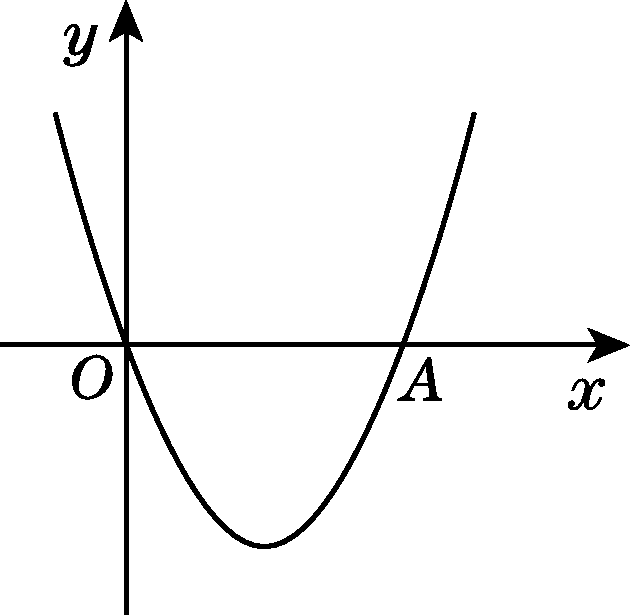
如图，在直角坐标系xOy中，二次函数y＝x²＋(2k－1)x＋k＋1的图象与x轴相交于O，A两点．

(1)求这个二次函数的解析式；

(2)在这条抛物线的对称轴右边的图象上有一点B，使△AOB的面积等于6，求点B的坐标；

(3)对于(2)中的点B，在此抛物线上是否存在点P，使∠POB＝90°？若存在，求出点P的坐标，并求出△POB的面积；若不存在，请说明理由．

知识点：试卷08

参考答案：见解析

解析：

解：(1)∵函数的图象与x轴相交于O，

∴0＝k＋1.

∴k＝－1.

∴y＝x²－3x.

(2)设B点的坐标为(x₀，y₀)．

∵△AOB的面积等于6，

∴2(1)AO·|y₀|＝6.

当x²－3x＝0时，即x(x－3)＝0，解得x＝0或3.

∴AO＝3.

∴|y₀|＝4，即|x₀²－3x₀|＝4.化简得(舍去)．

解得x₀＝4或x₀＝－1(舍去)．

当x₀＝4时，y₀＝x₀²－3x₀＝4，∴点B的坐标为(4，4)．

(3)假设存在点P.设符合条件的点P的坐标为(x₁，x₁²－3x₁)

∵点B的坐标为(4，4)，

∴∠BOA＝45°，BO＝

当∠POB＝90°时，易得点P在直线y＝－x上，

∴x₁²－3x₁＝－x₁.

解得x₁＝2或x₁＝0(舍去)．

∴x₁²－3x₁＝－2.

∴在抛物线上存在点P，使∠POB＝90°，且点P的坐标为(2，－2)．

∴OP＝

∴△POB的面积为2(1)PO·BO＝＝8.