九年级（上）期末数学试卷集（328题）

---

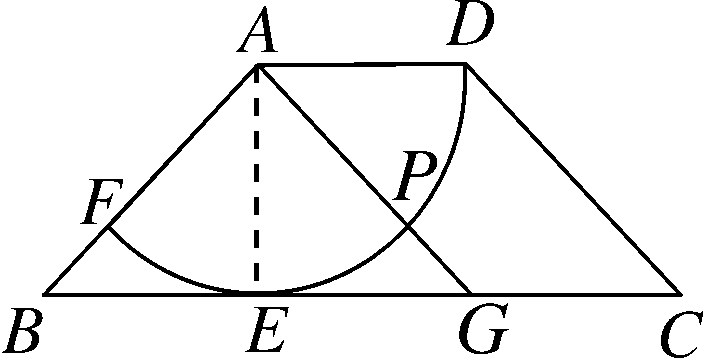
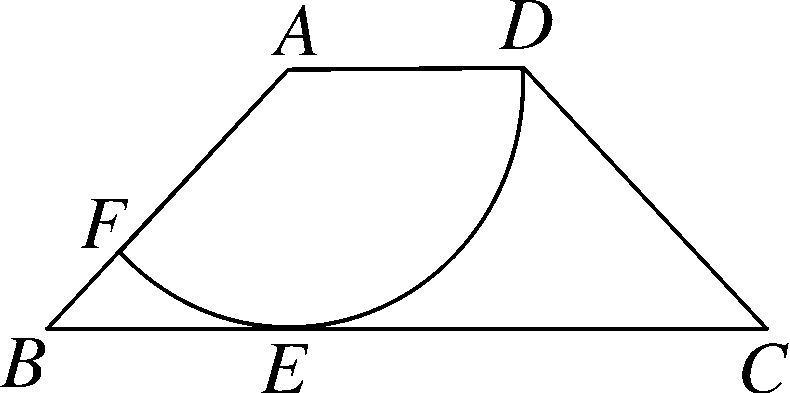
(10分)如图，在四边形ABCD中，AD∥BC，AD＝2，AB＝2√2，以点A为圆心，AD为半径的圆与BC相切于点E，交AB于点F.

(1)求∠ABE的大小及DEF(︵)的长度；

(2)在BE的延长线上取一点G，使得DE(︵)上的一个动点P到点G的最短距离为2√2－2，求BG的长．

知识点：试卷13

参考答案：见解析

解析：

解：（1）连接AE，如图，∵以AD为半径的圆与BC相切于点E，∴AE⊥BC，AE＝AD＝2.（1分）在Rt△AEB中，AE＝2，AB＝2√2，∴BE＝2，即△ABE是等腰直角三角形，∴∠ABE＝45°.（3分）∵AD∥BC，∴∠DAB＋∠ABE＝180°，∴∠DAB＝135°，∴DEF(︵)的长度为；（5分）

（2）如图，根据两点之间线段最短，可得当A，P，G三点共线时PG最短，（7分）此时AG＝AP＋PG＝2＋2√2－2＝2√2，∴AG＝AB.（9分）∵AE⊥BG，∴BE＝EG.∴BG＝2BE＝4.（10分）