九年级（上）期末数学试卷集（328题）

---

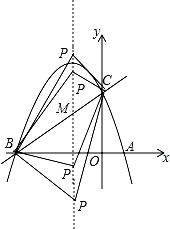
如图，已知抛物线y=ax²+bx+c（a≠0）的对称轴为直线x=﹣1，且抛物线经过A（1，0），C（0，3）两点，与x轴交于点B．

（1）若直线y=mx+n经过B、C两点，求直线BC和抛物线的解析式；

（2）在抛物线的对称轴x=﹣1上找一点M，使点M到点A的距离与到点C的距离之和最小，求出点M的坐标；

（3）设点P为抛物线的对称轴x=﹣1上的一个动点，求使△BPC为直角三角形的点P的坐标．

知识点：试卷04

参考答案：见解析

解析：

【考点】二次函数综合题．

【专题】压轴题．

【分析】（1）先把点A，C的坐标分别代入抛物线解析式得到a和b，c的关系式，再根据抛物线的对称轴方程可得a和b的关系，再联立得到方程组，解方程组，求出a，b，c的值即可得到抛物线解析式；把B、C两点的坐标代入直线y=mx+n，解方程组求出m和n的值即可得到直线解析式；

（2）设直线BC与对称轴x=﹣1的交点为M，则此时MA+MC的值最小．把x=﹣1代入直线y=x+3得y的值，即可求出点M坐标；

（3）设P（﹣1，t），又因为B（﹣3，0），C（0，3），所以可得BC²=18，PB²=（﹣1+3）²+t²=4+t²，PC²=（﹣1）²+（t﹣3）²=t²﹣6t+10，再分三种情况分别讨论求出符合题意t值即可求出点P的坐标．

【解答】解：（1）依题意得：，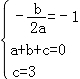

解之得：，

∴抛物线解析式为y=﹣x²﹣2x+3

∵对称轴为x=﹣1，且抛物线经过A（1，0），

∴把B（﹣3，0）、C（0，3）分别代入直线y=mx+n，

得，

解之得：，

∴直线y=mx+n的解析式为y=x+3；

 

（2）设直线BC与对称轴x=﹣1的交点为M，则此时MA+MC的值最小．

把x=﹣1代入直线y=x+3得，y=2，

∴M（﹣1，2），

即当点M到点A的距离与到点C的距离之和最小时M的坐标为（﹣1，2）；

 

（3）设P（﹣1，t），

又∵B（﹣3，0），C（0，3），

∴BC²=18，PB²=（﹣1+3）²+t²=4+t²，PC²=（﹣1）²+（t﹣3）²=t²﹣6t+10，

①若点B为直角顶点，则BC²+PB²=PC²即：18+4+t²=t²﹣6t+10解之得：t=﹣2；

②若点C为直角顶点，则BC²+PC²=PB²即：18+t²﹣6t+10=4+t²解之得：t=4，

③若点P为直角顶点，则PB²+PC²=BC²即：4+t²+t²﹣6t+10=18解之得：t₁=，t₂=；

综上所述P的坐标为（﹣1，﹣2）或（﹣1，4）或（﹣1，） 或（﹣1，）．

 

【点评】本题综合考查了二次函数的图象与性质、待定系数法求函数（二次函数和一次函数）的解析式、利用轴对称性质确定线段的最小长度、难度不是很大，是一道不错的中考压轴题．