九年级（上）期末数学试卷集（328题）

---

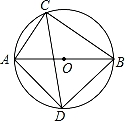
如图，⊙O的直径AB的长为10，弦AC的长为5，∠ACB的平分线交⊙O于点D．

（1）求的长．

（2）求弦BD的长．

 

知识点：试卷04

参考答案：见解析

解析：

【考点】圆周角定理；含30度角的直角三角形；等腰直角三角形；弧长的计算．

【分析】（1）首先根据AB是⊙O的直径，可得∠ACB=∠ADB=90°，然后在Rt△ABC中，求出∠BAC的度数，即可求出∠BOC的度数；最后根据弧长公式，求出的长即可．

（2）首先根据CD平分∠ACB，可得∠ACD=∠BCD；然后根据圆周角定理，可得∠AOD=∠BOD，所以AD=BD，∠ABD=∠BAD=45°；最后在Rt△ABD中，求出弦BD的长是多少即可．

【解答】解：（1）如图，连接OC，OD，，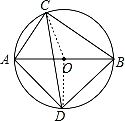

∵AB是⊙O的直径，

∴∠ACB=∠ADB=90°，

在Rt△ABC中，

∵，

∴∠BAC=60°，

∴∠BOC=2∠BAC=2×60°=120°，

∴的长=．

 

（2）∵CD平分∠ACB，

∴∠ACD=∠BCD，

∴∠AOD=∠BOD，

∴AD=BD，

∴∠ABD=∠BAD=45°，

在Rt△ABD中，

BD=AB×sin45°=10×．

【点评】（1）此题主要考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半，要熟练掌握．

（2）此题还考查了含30度角的直角三角形，以及等腰直角三角形的性质和应用，要熟练掌握．

（3）此题还考查了弧长的求法，要熟练掌握，解答此题的关键是要明确：①弧长公式：l=（弧长为l，圆心角度数为n，圆的半径为R）．②在弧长的计算公式中，n是表示1°的圆心角的倍数，n和180都不要带单位．