九年级（上）期末数学试卷集（328题）

---

如图1，在Rt△ABC中，∠B=90°，BC=2AB=8，点D、E分别是边BC、AC的中点，连接DE，将△EDC绕点C按顺时针方向旋转，记旋转角为α．

 

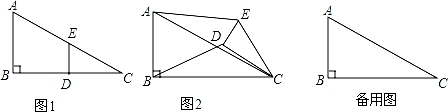
（1）问题发现

①当α=0°时， =　　；②当α=180°时， =　　．

（2）拓展探究

试判断：当0°≤α＜360°时，的大小有无变化？请仅就图2的情形给出证明．

（3）问题解决

当△EDC旋转至A，D，E三点共线时，直接写出线段BD的长．

知识点：试卷04

参考答案：见解析

解析：

【考点】几何变换综合题．

【专题】压轴题．

【分析】（1）①当α=0°时，在Rt△ABC中，由勾股定理，求出AC的值是多少；然后根据点D、E分别是边BC、AC的中点，分别求出AE、BD的大小，即可求出的值是多少．

②α=180°时，可得AB∥DE，然后根据，求出的值是多少即可．

（2）首先判断出∠ECA=∠DCB，再根据，判断出△ECA∽△DCB，即可求出的值是多少，进而判断出的大小没有变化即可．

（3）根据题意，分两种情况：①点A，D，E所在的直线和BC平行时；②点A，D，E所在的直线和BC相交时；然后分类讨论，求出线段BD的长各是多少即可．

【解答】解：（1）①当α=0°时，

∵Rt△ABC中，∠B=90°，

∴AC=，

∵点D、E分别是边BC、AC的中点，

∴，

∴．

 

②如图1，，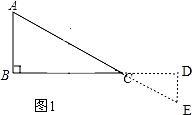

当α=180°时，

可得AB∥DE，

∵，

∴=．

故答案为：．

 

（2）如图2，，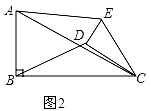

当0°≤α＜360°时，的大小没有变化，

∵∠ECD=∠ACB，

∴∠ECA=∠DCB，

又∵，

∴△ECA∽△DCB，

∴．

 

（3）①如图3，，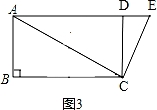

∵AC=4，CD=4，CD⊥AD，

∴AD==，

∵AD=BC，AB=DC，∠B=90°，

∴四边形ABCD是矩形，

∴．

 

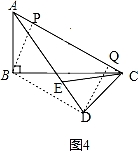
②如图4，连接BD，过点D作AC的垂线交AC于点Q，过点B作AC的垂线交AC于点P，

，

∵AC=4，CD=4，CD⊥AD，

∴AD==，

∵点D、E分别是边BC、AC的中点，

∴DE==2，

∴AE=AD﹣DE=8﹣2=6，

由（2），可得

，

∴BD==．

综上所述，BD的长为4或．

【点评】（1）此题主要考查了几何变换综合题，考查了分析推理能力，考查了分类讨论思想的应用，考查了数形结合思想的应用，要熟练掌握．

（2）此题还考查了相似三角形、全等三角形的判定和性质的应用，要熟练掌握．

（3）此题还考查了线段长度的求法，以及矩形的判定和性质的应用，要熟练掌握．