第1081题 购买—更新改造—出售模式和购买—更新改造—出租—出售模式这两种模式中，它们的不同点在于现金流出中后者包含运营成本而前者不包含。

参考答案：对

第1082题 从投资者的角度来看，资金的增值特性使其具有时间价值。（ ）

参考答案：对

第1083题 利率是资金时间价值的一种标志。（ ）

参考答案：对

第1084题 认为利率水平是由货币的供给与需求决定的代表性理论是马克思的利率决定理论（ ）

参考答案：错

解析：

是流动性偏好利率理论。

第1085题 资金一旦用于投资就不能用于即期消费，所以，从消费者的角度来看，资金的时间价值体现为放弃即期消费的损失所应得到的必要补偿。（ ）

参考答案：对

第1086题 当每年的计息周期数等于1时，名义利率与实际利率相等。（ ）

参考答案：对

第1087题 下列关于资金等效值概念的表述中，正确的是（ ）。

A.时值是资金运动起点的金额

B.终值是资金运动结束的金额

C.资金等值是指与某一时点上一定金额的实际价值相等的另一时点的价值

D.不同时点发生的绝对值相等的资金具有相同的价值

参考答案：C

解析：

现值是资金运动起点的金额，终值是资金运动结束时与现值等值的金额。

第1088题 某家庭向银行申请了一笔等额还本付息的个人住房抵押贷款，其月供为2850元，月利率为0．625%，则该抵押贷款的实际年利率为（ ）。

A.7．50%

B.7．56%

C.7．71%

D.7．76%

参考答案：D

解析：

i=（1＋0.625%）12－1=7.76%。

第1089题 银行为某家庭提供了一笔总额10万元、期限10年、年利率6%的住房抵押贷款。若采用月还款常数为0．7%的还款方式，并在最后1个月还清所余本息。则相对于按月等额还款方式，该家庭在还贷期间，除最后1个月外，其他各月的月供负担减少了（ ）元。

A.137．5

B.410．2

C.432．2

D.452．2

参考答案：B

解析：

月等额还款金额＝10×0．7%＝700（元），月利率＝6%/12=0．5%， ，则A＝1110．21元，1110．21－700＝410．21（元）。

第1090题 现有一套总售价为11万元的住宅，八成15年按揭，按年贷款利率6%计，月还款额为（ ）元。

A.439

B.1230

C.743

D.928

参考答案：C

解析：

运用公式        ，A=11´0.8´ 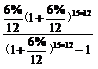   =743（元）。

第1091题 美国某家庭于2005年购买住房时申请了一笔20万美元的贷款，贷款方式为“2/28”。第一年和第二年的年利率为7．5%，两年后的年利率调整为8．5%，则该家庭在第28个月的月还款额为（ ）美元。

A.1250

B.1398

C.1416

D.1562

参考答案：D

解析：

20万贷款，28年的贷款期限，利用等额序列支付资金回收系数公式计算可得。

第1092题 某家庭以30万元购买了一套住宅，银行为其提供了15年期的住房抵押贷款，该贷款的年利率为6%，按月等额还款，如果该家庭于第6年初一次提前偿还贷款本金5万元，则从第6年开始的抵押贷款月还款额将减少（ ）元。

A.544．10

B.555．10

C.1776．32

D.2109．38

参考答案：B

解析：

将第6年初的5万元看作P，在余下的10年中每月等额还款数就是从第6年开始的抵押贷款月还款额减少值。运用公式 可得： ＝555．10（元）。注意：公式中的n是10而不是9，因为第6年初等于第5年末。做这种题一定要画一个现金流量图。

第1093题 时值是资金运动过程中某一时间点上的金额。（ ）

参考答案：错

解析：

资金运动过程中某一时间点上与现值等值的金额称为时值。

第1094题 假定年利率为10%，2008年初的100元与2008年年末的110元的实际经济价值是相等的。（ ）

参考答案：对

第1095题 在资金等效值计算过程中，终值是指资金运动结束时发生的实际金额。（ ）

参考答案：错

解析：

终值是指资金运动结束时与现值等值的金额。

第1096题 某家庭准备以抵押贷款方式购买一套住房。该家庭月总收入7000元，最多能以月收入的25%支付住房贷款的月还款额。年贷款利率为6%，最长贷款期限20年，最低首付款为房价的30%，若采用按月等额偿还方式，问：1）该家庭能购买住房的最高总价是多少？若第5年末银行贷款利率上调为9%，为保持原月偿还不变，则：2）该家庭需在第6年初一次性提前偿还贷款多少元？3）如果不提前偿还贷款，则需将贷款期限延长多少年？

参考答案：见解析

解析：

1．计算该家庭购买住房的最高总价

月还款额：A＝7000×25%＝1750（元）（0．5分）

最高贷款额：＝＝244266．35（元）≈24．43（万元）（1分）

（本步计算中，i取0．5%，n取240，给0．5分）

购买住房的最高总价：24．43/70%＝34．9（万元）（0．5分）

2．计算第6年初一次性提前偿还款

解法1

第5年末尚余贷款本金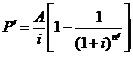：＝＝207381．15（元）≈20．74（万元）

（本步计算中，i取0．5%，n′取180，给0．5分）

调息后的月还款额：

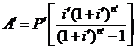＝207381．15×＝2103．40（元）（1分）

（本步计算中，i′取0．75%，n′取180，给0．5分）

调息后每月增加的还款额：2103．40－1750．0＝353．40（元）（0．5分）

提前还款额：

＝34842．91（元）≈3．48（万元）（1分）

解法2  设提前还款额为P″，则有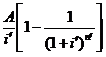＋P″＝P′（1分）

第5年末尚余贷款本金：

＝

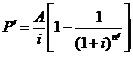＝207381．15（元）≈20．74（万元）（1分）

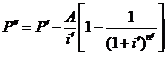＝207381．15－（1分）

＝34842．68（元）≈3．48（万元）（0．5分）

3．贷款延长期的计算

设从第5年末开始的还款期为Ｘ月，则有

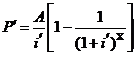（0．5分）

207381．15＝（0．5分）

（1＋0．75%）^Ｘ＝8．99，Ｘ＝294（月）（0．5分）

延长期：294－180＝114（月）＝9．5（年）（0．5分）

第1097题 某家庭估计在今后10年内的月收入为16000元，如果月收入的30％可以用于支付住房抵押贷款的月还款，在年贷款利率为12％的情况下，该家庭有偿还能力的最大抵押贷款额是多少？（月收入发生在月初）

参考答案：见解析

解析：

该家庭用于支付住房抵押贷款的月还款额为：16000×30％＝4800（元）

月利率＝12％/12＝1％

由于月收入为月初，先把其折到月末：4800×（1＋1％）＝4848（元）

利用公式P＝A/i［1－1/（1＋i）ⁿ］，求得该家庭有偿还能力的最大抵押贷款额为：

P＝4848［（1＋1％）¹²⁰－1］/［1％（1＋1％）¹²⁰］＝337908．13（元）

第1098题 某家庭购买一套住宅，单价为3000元/平米，该家庭月收入6000元，其中30％可用来支付房款，银行可为其提供15年期的住房抵押贷款，贷款利率为6％，抵押贷款价值比例最大为80％，问根据该家庭的支付能力最多可以购买多少平米的住宅？
解题思路：此题由题意分析可知，是要求Ｐ值。选用净收益每年不变有限年期公式，将其中的报酬率Ｙ换成i。

参考答案：见解析

解析：

（1）该家庭每月能支付的房款A＝6000×30％＝1800（元）

（2）n＝15×12＝180月，i＝6％/12＝0．5％

（3）该家庭能承受的抵押贷款额P＝A/i［1－1/（1＋i）ⁿ］

P＝1800/0．5％/［1－1/（1＋0．5％）¹⁸⁰］＝213306（元）

（4）该家庭能承受的购房总价值V＝213306/80％＝266633（元）

（5）该家庭的支付能力最多可以购买住宅面积S＝266633/3000＝88．88（平方米）。

第1099题 某投资者以4500元/平米的价格购买了一套建筑面积为120平米的住宅，并向银行申请了相当于70％的按月等额还款的抵押贷款，已知该项抵押贷款的年限为15年，年利率为12％，按月计息，如果该家庭拟于开始还款后的第10年年初一次偿清该项贷款的余额，问此时一次偿还的金额为多少？
解题思路：据题意是按月等额还款，选用运用净收益每年不变有限年期公式，将其中的报酬率Ｙ换成i，求出每月等额还款数Ａ。画出现金流量图，将“第10年初”看作计息起点0，第10年末就是1点，以此类推，第15年末的标记点为6，则t＝6×12＝72（月），注意t＝5×12＝60（月）的表述是错误的。这也是在本门教材中一个难点和容易出错的点，一定要注意选对计息期的起点和终点。

参考答案：见解析

解析：

（1）已知P＝4500×120×70％＝378000（元），n＝15×12＝180（月），

t＝6×12＝72（月），i＝12％/12＝1％

（2）A＝P×［i（1＋i）ⁿ］/［（1＋i）ⁿ－1］＝378000×1％×（1＋1％）¹⁸⁰/［（1＋1％）¹⁸⁰－1］＝4536．64（元）

（3）第10年初拟一次偿还的金额为：

P₁₀＝A/i［1－1/（1＋i）^t］＝4536．64/1％［1－1/（1＋1％）⁷²］＝232050．91（元）

第10年初一次偿还的金额为232051元。

第1100题 某家庭估计在今后10年内的月收入为8000元，如果其月收入的40％可以用来支付住房抵押贷款的月还款额，在年贷款利率为6％的情况下，该家庭有偿还能力的最大抵押贷款额是多少？

参考答案：见解析

解析：

该家庭每月用于住房支出的数额A＝8000×40％＝3200（元）

i＝6％／12＝0．5％

n＝10×12＝120（月）

最高贷款额P＝A×｛［（1＋i）ⁿ－1］／［i（1＋i）ⁿ］｝

P＝3200×｛［（1＋0．5％）¹²⁰－1］／［0．5％（1＋0．5％）¹²⁰］｝＝288235．05（元）