“微信扫一扫”进入考试题库练习及模拟考试
初中数学八年级上册试题库(555题)
A.18
B.30
C.24
D.27
参考答案:D
第122题
如图,点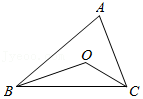
A.\(58^\circ \)
B.\(64^\circ \)
C.\(122^\circ \)
D.\(124^\circ \)
参考答案:C
A.10
B.8
C.6
D.4
参考答案:C
参考答案:\(1\)
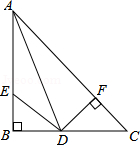
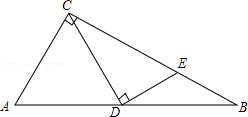
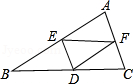
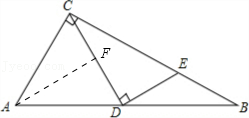
参考答案:\(\because \angle B = 90^\circ \),\(\therefore BD \bot AB\)。\(\because AD\)为\(\angle BAC\)的平分线,且\(DF \bot AC\),\(\therefore DB = DF\)。在\({\rm{Rt}}\Delta {\rm{BDE}}\)和\({\rm{Rt}}\Delta {\rm{FDC}}\)中,\(\left\{ {\begin{array}{*{20}{l}}
{DE = DC} \\
{DB = DF}
\end{array}} \right.\),\(\therefore {\rm{Rt}}\Delta {\rm{BDE}} \cong {\rm{Rt}}\Delta {\rm{FDC}}({\rm{HL}})\),\(\therefore BE = CF\)。
参考答案:
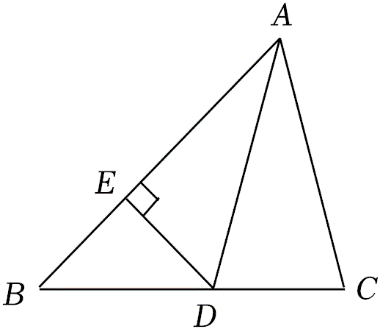
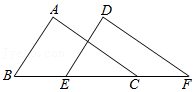
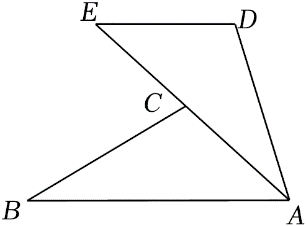
证明:如图,过点
在
{\angle ACF = \angle DEC} \\
{\angle AFC = \angle CDE} \\
{AC = CE}
\end{array}} \right.\)
A.\(50^\circ \)
B.\(60^\circ \)
C.\(65^\circ \)
D.\(120^\circ \)
参考答案:B
参考答案:①\(BC = EF\)(\(BE = CF\))②\(\angle A = \angle D\)③\(\angle ACB = \angle F\)(\(AC//DF\))
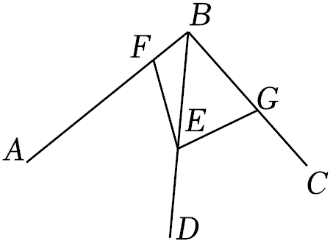
A.\(\angle BFE + \angle BGE = 90^\circ \)
B.\(\angle BFE + \angle BGE = 180^\circ \)
C.\(\angle BFE = 2\angle BGE\)
D.\(\angle BFE - \angle BGE = 90^\circ \)
参考答案:B
第131题
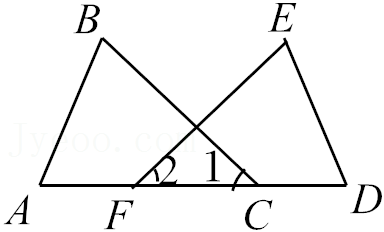
如图,已知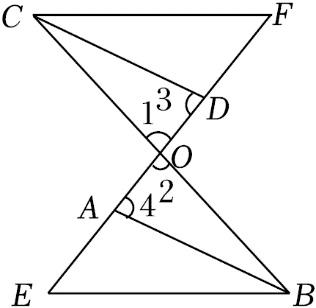
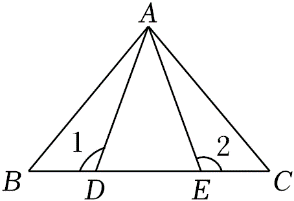
参考答案:证明:\(\because AB//CD\),\(\therefore \angle 3 = \angle 4\),在\(\Delta ABO\)和\(\Delta DCO\)中,\(\left\{ {\begin{array}{*{20}{l}}
{\angle 3 = \angle 4} \\
{OA = OD} \\
{\angle 1 = \angle 2}
\end{array}} \right.\),\(\therefore \Delta ABO \cong \Delta DCO(ASA)\),\(\therefore AB = CD\),\(\because \angle 3 = \angle 4\),\(\therefore \angle CDF = \angle BAE\),在\(\Delta ABE\)和\(\Delta DCF\)中,\(\left\{ {\begin{array}{*{20}{l}}
{AE = DF} \\
{\angle BAE = \angle CDF} \\
{AB = CD}
\end{array}} \right.\),\(\therefore \Delta ABE \cong \Delta DCF(SAS)\),\( EB=CF\)。
第132题
求证:
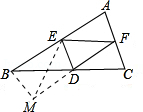
参考答案:证明:正五边形\(ABCDE\)中,\(AB = BC\),\(\angle ABM = \angle C\),在\(\Delta ABM\)和\(\Delta BCN\)中\(\left\{ {\begin{array}{*{20}{l}}
{AB = BC} \\
{\angle ABM = \angle C} \\
{BM = CN}
\end{array}} \right.\),\(\therefore \Delta ABM \cong \Delta BCN(SAS)\);
第133题
求
参考答案:\(\because \Delta ABM \cong \Delta BCN\),\(\therefore \angle BAM = \angle CBN\),\(\therefore \angle APN = \angle BAM + \angle ABP\)\( = \angle CBN + \angle ABP\)\( = \angle ABC\)\( = \frac{{(5 - 2) \times 180^\circ }}{5}\)\( = 108^\circ \)。
参考答案:
证明:延长
在
BD = CD \\
\angle BDM = \angle FDC \\
MD = FD \\
\end{cases}\)
在
参考答案:\(80^\circ \)
A.\(44cm\)
B.\(45cm\)
C.\(46cm\)
D.\(48cm\)
参考答案:B
参考答案:①\(BC = EF\)②\(\angle A = \angle D\)③\(\angle B = \angle E\)
A.\(68^\circ \)
B.\(69^\circ \)
C.\(71^\circ \)
D.\(72^\circ \)
参考答案:C
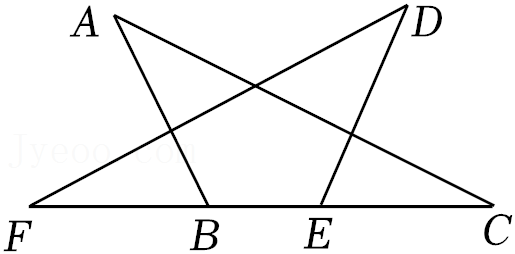
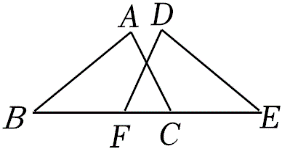
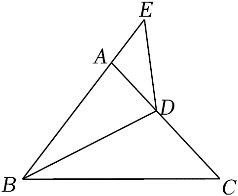
参考答案:证明:\(\because AB//ED\),\(\therefore \angle EAB = \angle E\),\(\because \angle DAB = \angle BAE + \angle B\),\(\angle DAB = \angle BAE + \angle DAE\),\(\therefore \angle B = \angle DAE\),在\(\Delta ABC\)和\(\Delta EAD\)中,\(\left\{ {\begin{array}{*{20}{l}}
{\angle B = \angle DAE} \\
{AB = EA} \\
{\angle BAC = \angle E}
\end{array}} \right.\),\(\therefore \Delta ABC \cong \Delta EAD(ASA)\),\(\therefore AC = ED\).
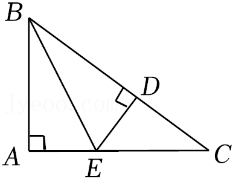
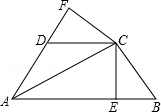
参考答案:证明:(1)\(\because AC\)是角平分线,\(CE \bot AB\)于\(E\),\(CF \bot AD\)于\(F\),\(\therefore CE = CF\),在\({\rm{Rt}}\Delta {\rm{BCE}}\)和\({\rm{Rt}}\Delta {\rm{DCF}}\)中,\(\left\{ {\begin{array}{*{20}{l}}
{BC = DC} \\
{CE = CF}
\end{array}} \right.\)\(\therefore \Delta BCE \cong \Delta DCF(HL)\);(2)在\({\rm{Rt}}\Delta {\rm{FAC}}\)和\({\rm{Rt}}\Delta {\rm{EAC}}\)中,\(\left\{ {\begin{array}{*{20}{l}}
{AC = AC} \\
{CE = CF}
\end{array}} \right.\),\(\therefore Rt\Delta FAC \cong Rt\Delta EAC(HL)\),\(\therefore AF = AE\),\(\because \Delta BCE \cong \Delta DCF\),\(\therefore BE = DF\),\(\therefore AB + AD = (AE + BE) + (AF - DF) = 2AE\)。