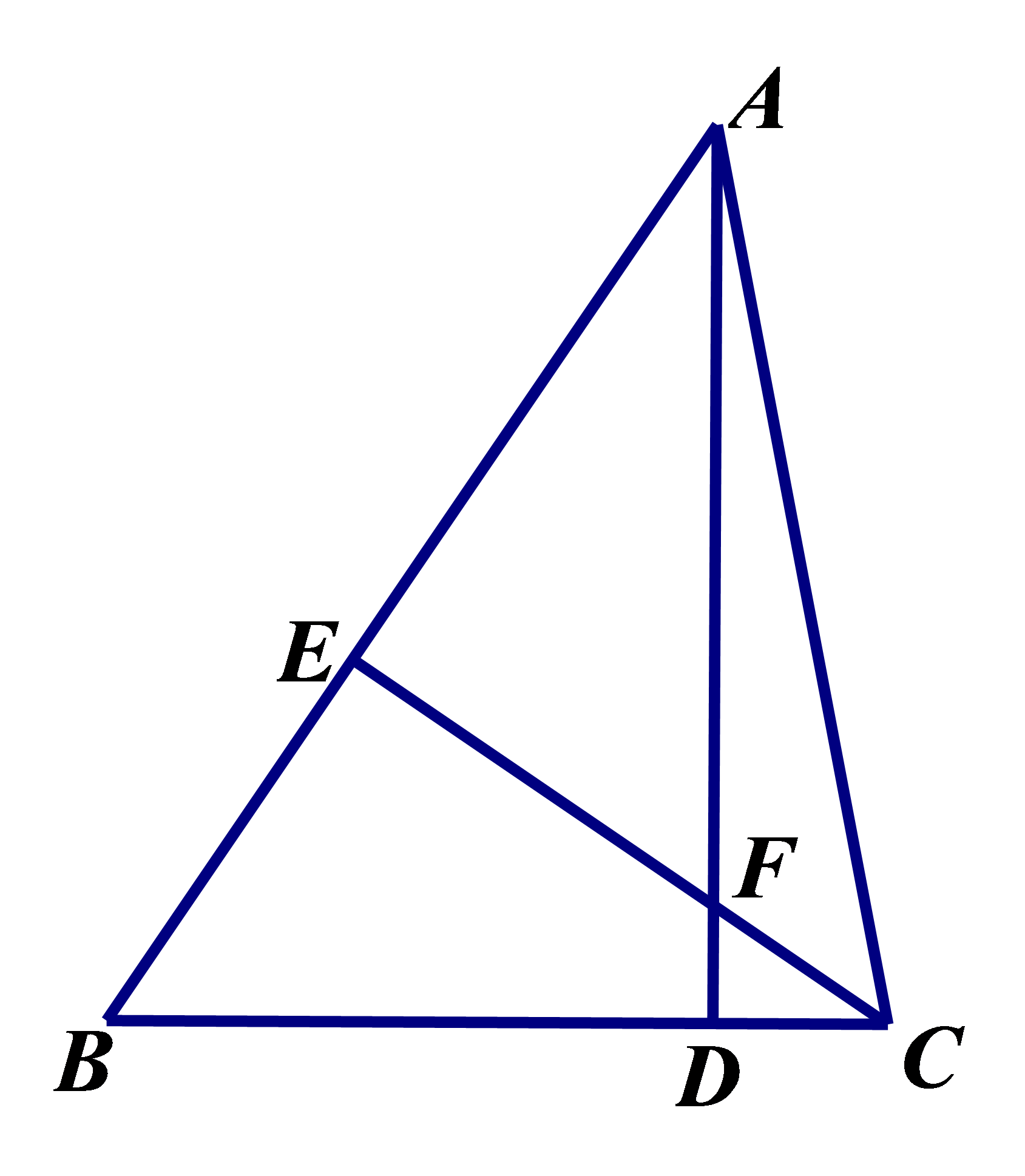“微信扫一扫”进入考试题库练习及模拟考试
初中数学八年级上册试题库(555题)
A.1
B.1.5
C.2
D.2.5
参考答案:A
第83题
已知,
A.\(△ABC≌△XYZ\)
B.\(△DEF≌△XYZ\)
C.\(∠C=∠Z\)
D.\(∠F=80°\)
参考答案:C
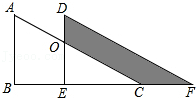
参考答案:
证明:连接
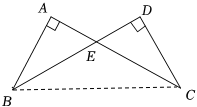
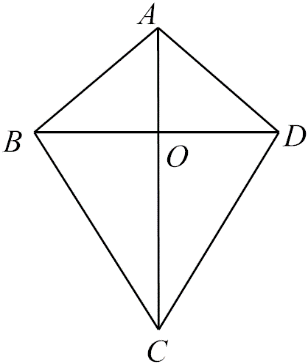
在
{AC = BD} \\
{BC = CB}
\end{array}} \right.\)
在
\begin{gathered}
\angle A = \angle D \\
\angle AEB = \angle DEC \\
\end{gathered} \\
{AB = DC}
\end{array}} \right.\)
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布日期:2022/7/17 15:34:21;用户:邓芸;邮箱:syxx019@xyh.com;学号:21059015
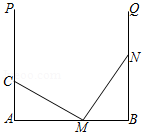
A.\(\Delta ABC \cong \Delta CDE\)
B.\(\angle CAB = \angle DCE\)
C.\(AB \bot CD\)
D.\(E\)为\(BC\)中点
参考答案:D
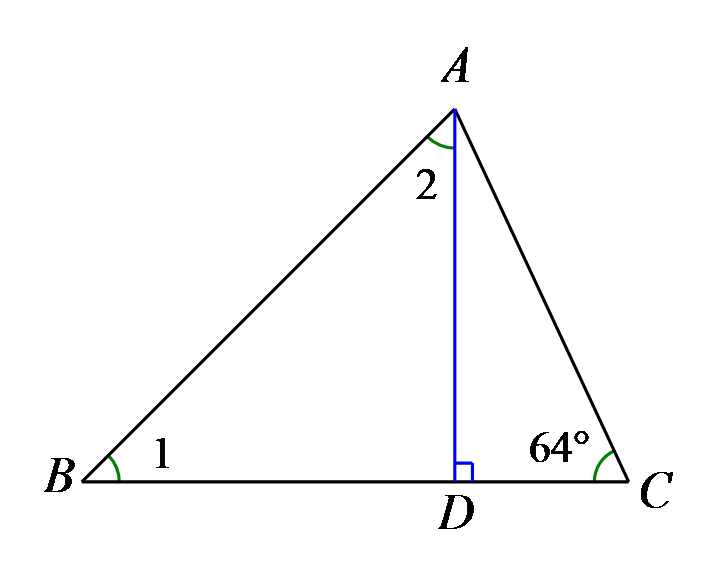
A.\(49^\circ \)
B.\(59^\circ \)
C.\(41^\circ \)
D.\(51^\circ \)
参考答案:C
A.\(50^\circ \)
B.\(55^\circ \)
C.\(60^\circ \)
D.\(70^\circ \)
参考答案:C
A.6
B.7
C.8
D.9
参考答案:C
第89题
如图,在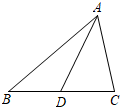
A.5
B.6
C.7
D.8
参考答案:A
A.1
B.2
C.3
D.5
参考答案:B
第91题
如图,在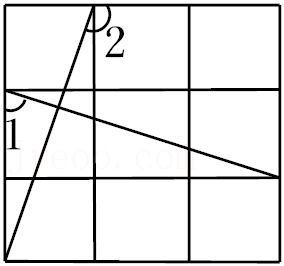
A.\(\angle 1 = \angle 2\)
B.\(\angle 2 = 2\angle 1\)
C.\(\angle 1 + \angle 2 = 90^\circ \)
D.\(\angle 1 + \angle 2 = 180^\circ \)
参考答案:D
第92题
如图,点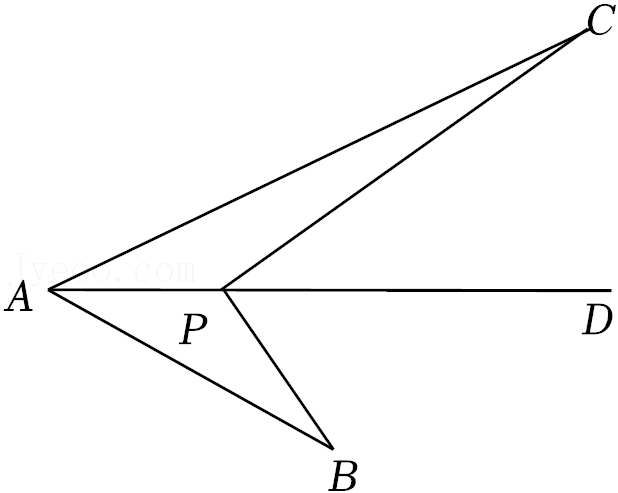
A.6
B.7
C.8
D.9
参考答案:A
参考答案:见解析
解析:
证明:延长
在
在
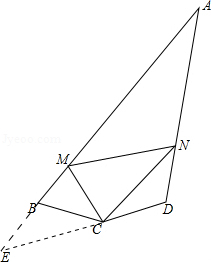
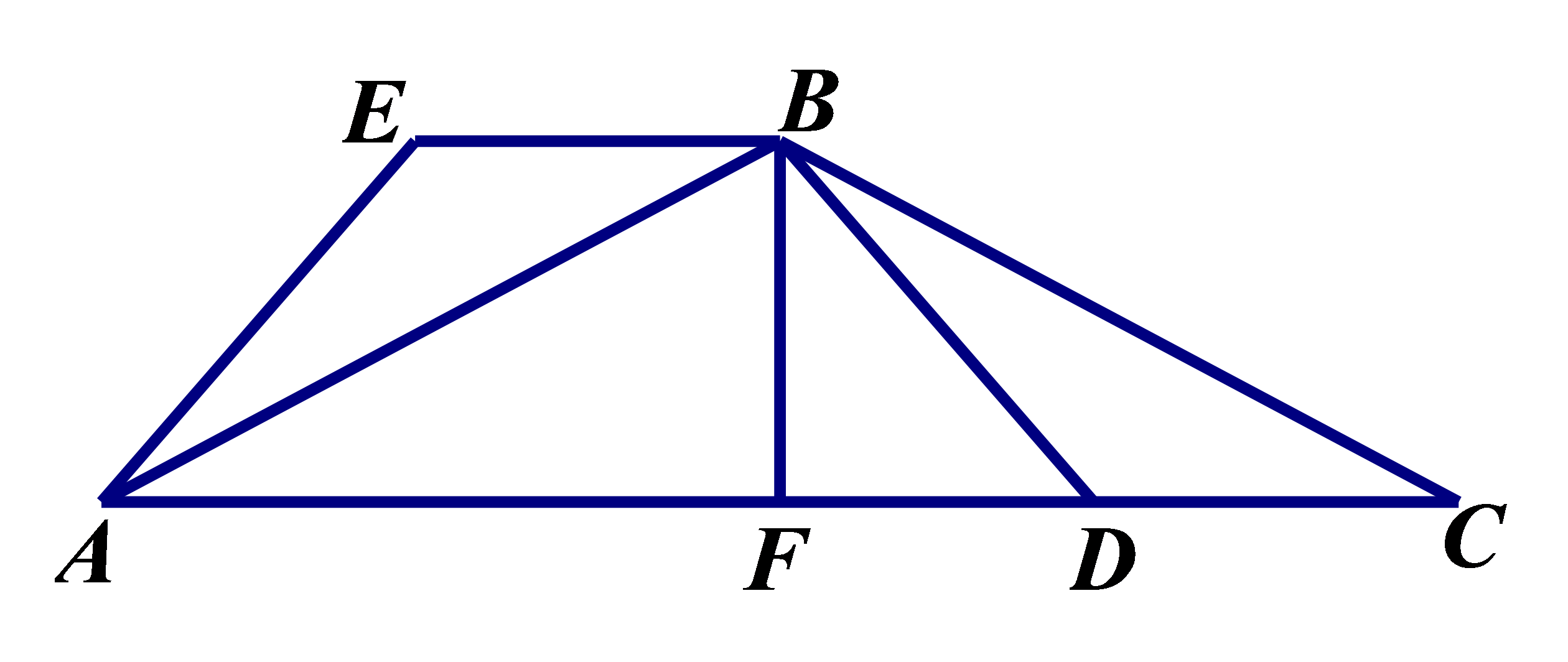
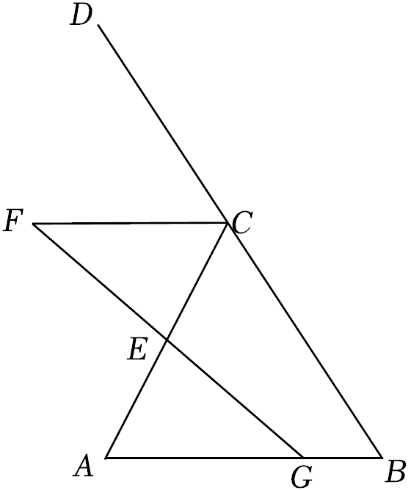
参考答案:证明:\(\because \angle B = \angle DCF\),\(\therefore CF//AB\),\(\therefore \angle FCA = \angle A\),\(\angle F = \angle FGA\),\(\because \)点\(E\)是\(AC\)的中点,\(\therefore AE = EC\),在\(\Delta AEG\)和\(\Delta CEF\)中,\(\left\{ {\begin{array}{*{20}{l}}
{\angle A = \angle FCA} \\
{\angle FGA = \angle F} \\
{AE = EC}
\end{array}} \right.\),\(\therefore \Delta AEG \cong \Delta CEF(AAS)\)。\(\because \Delta AEG \cong \Delta CEF\);\(\therefore CF = AG = 6\),\(\because AG = 3BG\),\(\therefore BG = 2\),\(\therefore AB = 8\),\(\therefore \Delta ABC\)的周长\( = AB + AC + BC = 28\)。
参考答案:线段\(AD\)与\(AG\)垂直且相等\(\because BE \bot AC\),\(CF \bot AB\),\(\therefore \angle HFB = \angle HEC = 90^\circ \),又\(\because \angle BHF = \angle CHE\),\(\therefore \angle ABD = \angle ACG\),在\(\Delta ABD\)和\(\Delta GCA\)中\(\left\{ {\begin{array}{*{20}{l}}
{AB = CG} \\
{\angle ABD = \angle ACG} \\
{BD = CA}
\end{array}} \right.\),\(\therefore \Delta ABD \cong \Delta GCA(SAS)\),\(\therefore AD = GA\)(全等三角形的对应边相等);\(\because \Delta ABD \cong \Delta GCA\),\(\therefore \angle ADB = \angle GAC\),又\(\because \angle ADB = \angle AED + \angle DAE\),\(\angle GAC = \angle GAD + \angle DAE\),\(\therefore \angle AED = \angle GAD = 90^\circ \),\(\therefore AD \bot GA\)。