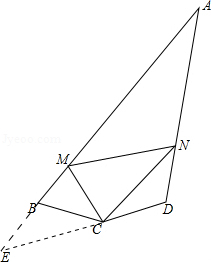
证明:延长\(AB\)至点\(E\),使得\(BE = DN\),连接\(CE\),
\(\because \)四边形\(ABCD\)中,\(\angle B + \angle D = 180^\circ \),\(\angle ABC + \angle CBE = 180^\circ \),
\(\therefore \angle CBE = \angle CDN\),
在\(\Delta CBE\)和\(\Delta CDN\)中,
\(\left\{ {\begin{array}{*{20}{l}} {CB = CD} \\\ {\angle CBE = \angle CDN} \\\ {BE = DN} \end{array}} \right.\),
\(\therefore \Delta CBE \cong \Delta CDN(SAS)\),
\(\therefore \angle BCE = \angle DCN\),\(CN = CE\),
\(\because \angle BCD = 150^\circ \),\(\angle MCN = 75^\circ \),
\(\therefore \angle MCE = \angle MCB + \angle BCE = \angle MCB + \angle DCN = 75^\circ \),
\(\therefore \angle MCN = \angle MCE\),
在\(\Delta ECM\)和\(\Delta NCM\)中,
\(\left\{ {\begin{array}{*{20}{l}} {MC = MC} \\\ {\angle MCN = \angle MCE} \\\ {CN = CE} \end{array}} \right.\),
\(\therefore \Delta ECM \cong \Delta NCM(SAS)\),
\(\therefore MN = ME = BM + BE = BM + DN\)。