第141题

如图，给出四个条件：①\(AE\)平分\(\angle BAD\)，②\(BE\)平分\(\angle ABC\)，③\(AE \bot EB\)，④\(AB = AD + BC\)．请你以其中3个作为条件，写出一个能推出\(AD//BC\)的正确命题，并给以证明。

参考答案：见解析

解析：

第142题

如图，在\({\rm{Rt}}\Delta {\rm{ABC}}\)中，\(\angle C = 90^\circ \)，\(DE\)是线段\(AB\)的垂直平分线，已知\(\angle CBD = \frac{1}{2}\angle ABD\)，则\(\angle A = \)___。

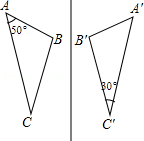
参考答案：\(36^\circ \)

第143题

如图，在\(\Delta ABC\)中，\(BC = 8\)，\(AB\)的中垂线交\(BC\)于\(E\)，\(AC\)的中垂线交\(BC\)于\(G\)，则\(\Delta AGE\)的周长等于 ___。

参考答案：8

第144题

如图，\({\rm{Rt}}\Delta {\rm{ABC}}\)中，\(\angle ACB = 90^\circ \)，分别以点\(A\)和点\(B\)为圆心，以相同的长（大于\(\frac{1}{2}AB)\)为半径作弧，两弧相交于点\(M\)和\(N\)，作直线\(MN\)交\(AB\)于点\(D\)，交\(BC\)于点\(E\)，若\(AC = 3\)，\(BC = 4\)，则\(DE\)等于 ___。

参考答案：\(\frac{{15}}{8}\)

第145题

如图，在\({\rm{Rt}}\Delta {\rm{ABC}}\)中，\(\angle C = 90^\circ \)，\(AB\)的垂直平分线交\(BC\)、\(AB\)于\(D\)，\(E\)，连接\(AD\)，\(\angle CAD = 20^\circ \)，则\(\angle B\)的度数是 ___。

参考答案：\(35^\circ \)

第146题

如图，在\(\Delta ABC\)中，\(DE\)是\(AC\)的垂直平分线，\(CE = 3cm\)，且\(\Delta ABD\)的周长为\(13cm\)，则\(\Delta ABC\)的周长为

\((\)　　\()cm\)。

A.19

B.13

C.10

D.16

参考答案：A

第147题

如图，在\(\Delta ABC\)中，\(\angle C = {90^o}\)，\(\angle B = {15^o}\)，\(AC = 3\)，\(AB\)的垂直平分线\(l\)交\(BC\)于点\(D\)，连接\(AD\)，则\(BC\)的长为 ___。

参考答案：\(6 + 3\sqrt 3 \)

第148题

如图，在\(\Delta ABC\)中，\(BD\)平分\(\angle ABC\)，过\(BC\)的中点\(E\)作\(BC\)的垂线交\(BD\)于点\(F\)，连接\(CF\)．若\(\angle A = 50^\circ \)，

\(\angle ACF = 40^\circ \)，则\(\angle CFD\)的度数为 ___。

参考答案：\(60^\circ \)

第149题

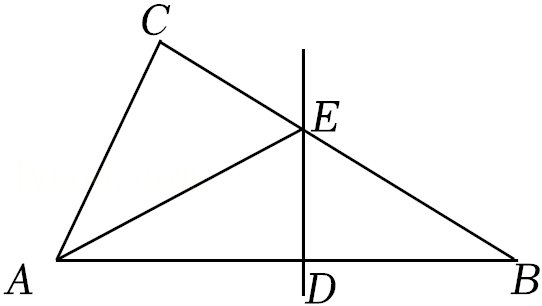
如图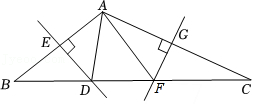，\(DE\)垂直平分\(AB\)，\(FG\)垂直平分\(AC\)，若\(\angle BAC = 110^\circ \)，则\(\angle DAF = \)___度。

参考答案：40

第150题

如图，\(\Delta ABC\)中，\(\angle C = 90^\circ \)，\(DE\)垂直平分\(AB\)，分别交\(AB\)、\(BC\)于点\(D\)、\(E\)，若\(\angle CAE = \angle B + 18^\circ \)，则\(\angle B\)的度数为 ___。

参考答案：\(24^\circ \)

第151题

\(\Delta ABC\)中，\(BC = 10\)，\(AB\)的垂直平分线与\(AC\)的垂直平分线分别交\(BC\)于点\(D\)，\(E\)，且\(DE = 4\)，则\(AD + AE\)

的值为\((\)　　\()\)。

A.6

B.14

C.6或14

D.8或12

参考答案：C

第152题

如图，在\(\Delta ABC\)中，边\(AC\)的垂直平分线交\(BC\)于点\(D\)，交\(AC\)于点\(E\)、已知\(\Delta ABC\)中与\(\Delta ABD\)的周长分别为20和13，则\(AE\)的长等于 ___。

参考答案：3.5

第153题

如图，有\(A\)、\(B\)、\(C\)三个居民小区的位置成三角形，现决定在三个小区之间修建一个购物超市，使超市到三个小区的距离相等，则超市应建在\((\)　　\()\)。

A.在\(AC\)，\(BC\)两边高线的交点处

B.在\(AC\)，\(BC\)两边中线的交点处

C.在\(AC\)，\(BC\)两边垂直平分线的交点处

D.在\(\angle A\)，\(\angle B\)两内角平分线的交点处在

参考答案：C

第154题

如图，平面内不共线三点\(A\)，\(B\)，\(C\)，操作如下：

（1）连接\(BC\)，以点\(B\)为圆心，以\(CB\)的长为半径画弧；

（2）连接\(AC\)，以点\(A\)为圆心，以\(AC\)的长为半径画弧，两弧相交于点\(D\)；

（3）连接\(CD\)，且过\(A\)，\(B\)作直线则\(A\)，\(B\)一定在线段\(CD\)的垂直平分线上，依据是：___。

参考答案：到线段\(CD\)两端点距离相等的点在\(CD\)的垂直平分线上

第155题

如图，在\(\Delta ABC\)中，\(BC\)边的垂直平分线\(MN\)交\(AC\)边于点\(D\)，交\(BC\)边于点\(E\)，连接\(BD\)，若\(CE = 4\)，

\(\Delta BDC\)的周长为18，求\(BD\)的长为 ___。

参考答案：5

第156题

直线\(l\)是一条河，\(P\)，\(Q\)是在\(l\)同侧的两个村庄．欲在\(l\)上的\(M\)处修建一个水泵站，向\(P\)，\(Q\)两地供水，

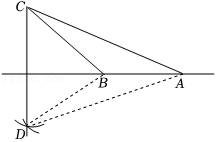
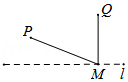
A.

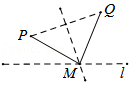
B.

C.

D.

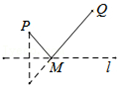
参考答案：C

第157题

下列图形中，是轴对称图形的有___。

①角 ②线段 ③等腰三角形 ④平行四边形 ⑤圆

参考答案：①②③⑤

第158题

\(△ABC\)与\(△DEF\)关于直线m对称，AB=4，BC=6，△DEF的周长是15，则AC=___。

参考答案：5

第159题

如图，\(△ABC\)和\(△{A}^{'}{B}^{'}{C}^{'}\)关于直线l对称，若∠A＝50°，∠C′＝30°，则∠B的度数为___。

参考答案：100°

第160题

如图所示，点P为∠AOB内一点，分别作出点P关于OA、OB的对称点P₁、P₂．连接P₁P₂交OA于M，交OB于N，若P₁P₂=6，则\(△PMN\)的周长为___。

参考答案：6