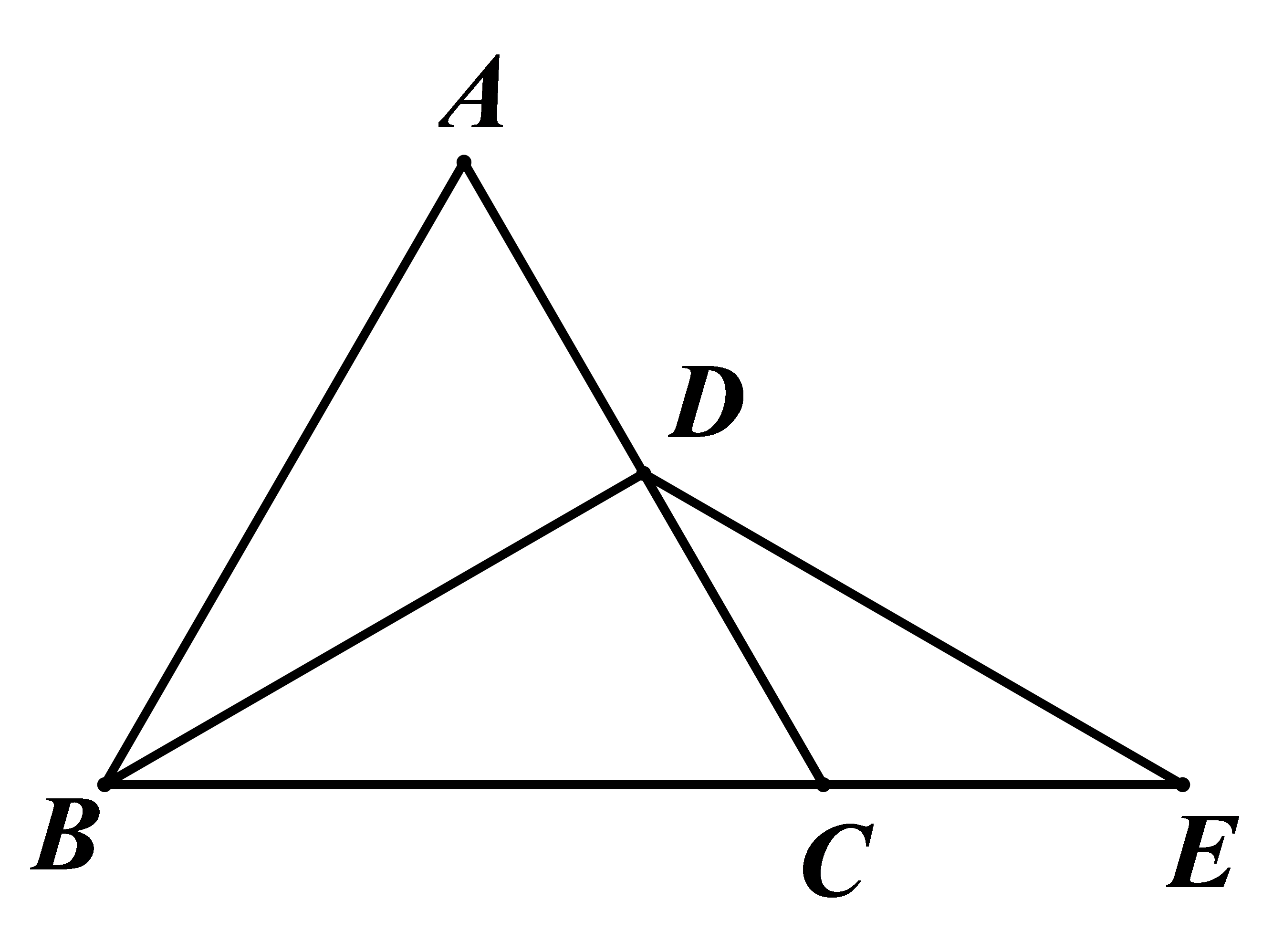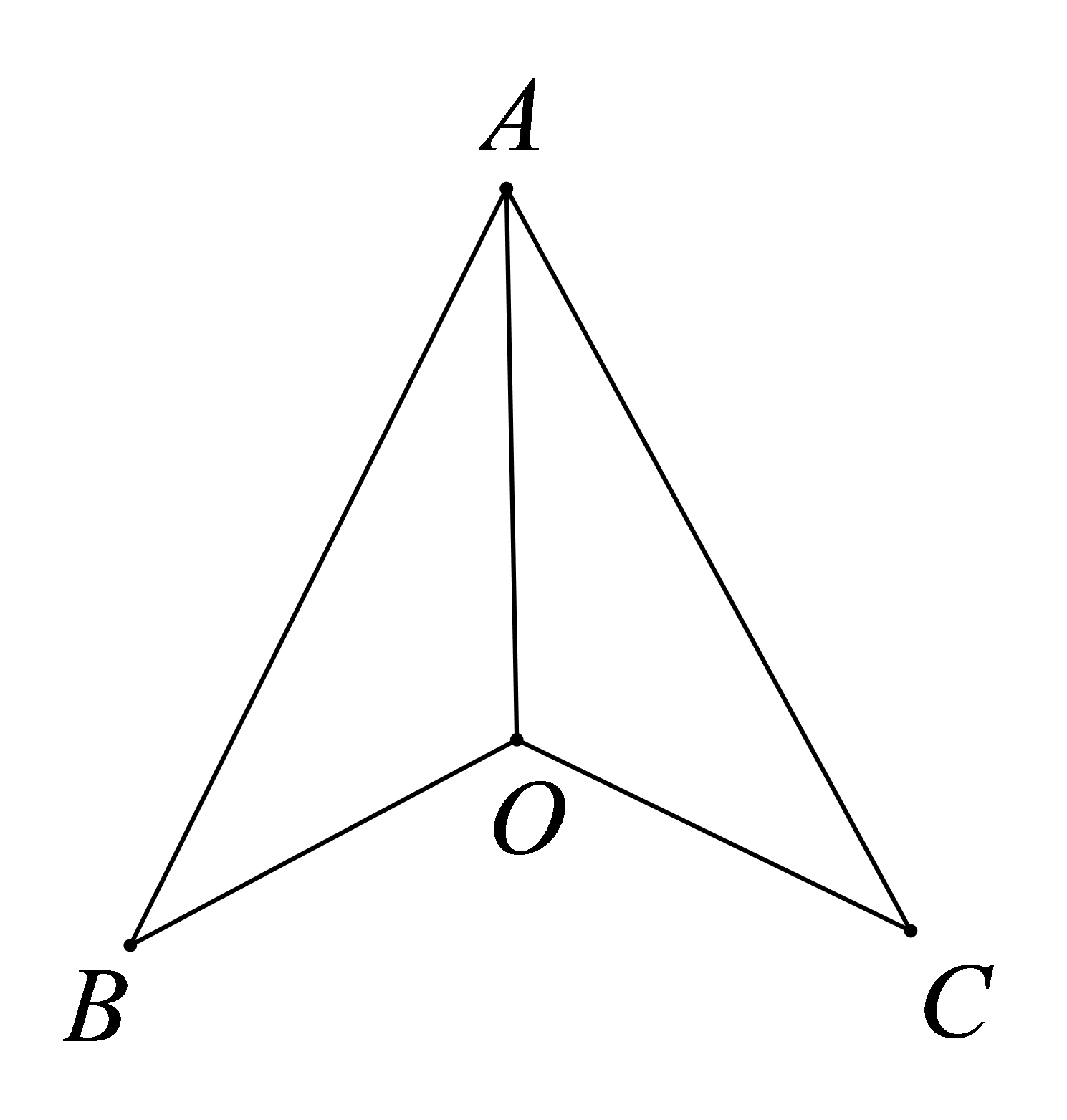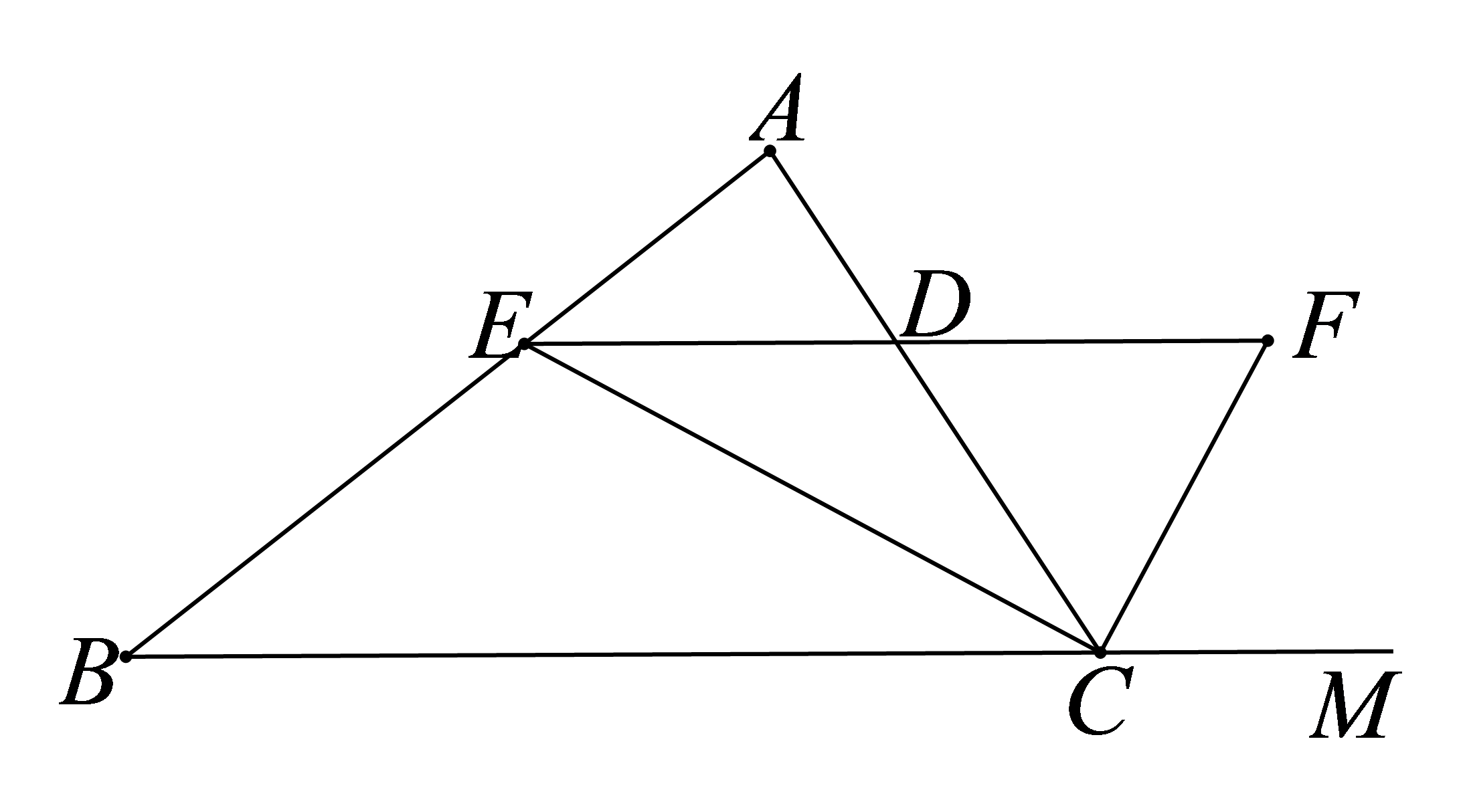“微信扫一扫”进入考试题库练习及模拟考试
初中数学八年级上册试题库(555题)
第181题
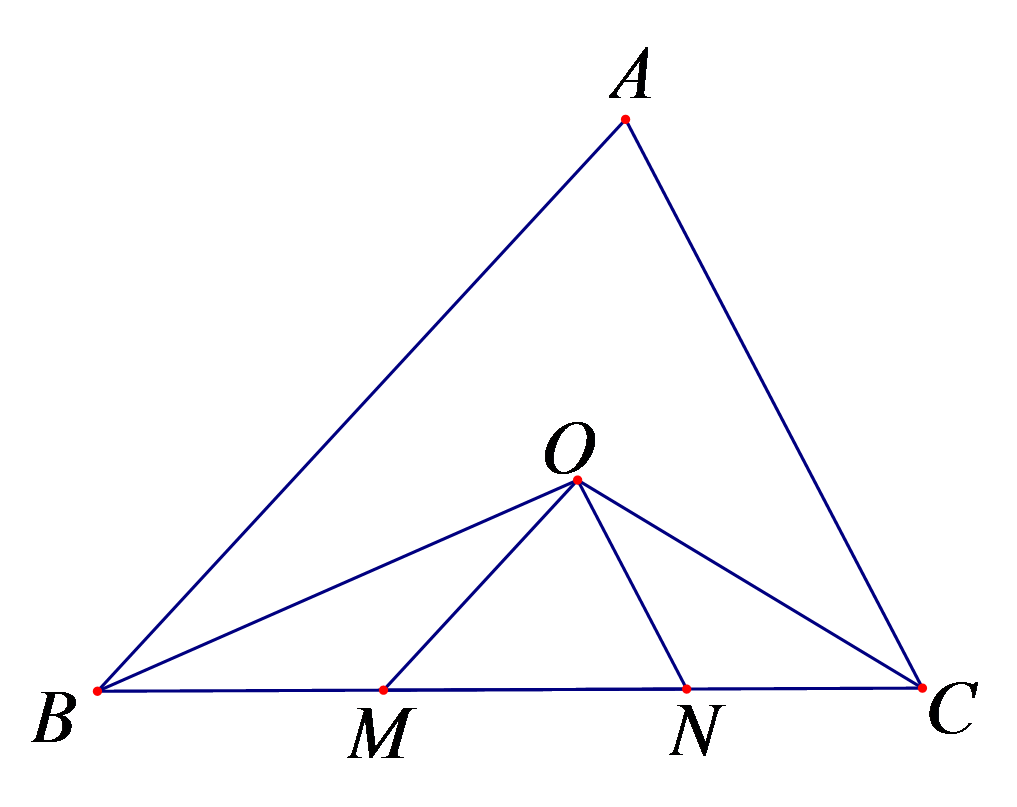
当α=150°时,试判断
参考答案:由\(\Delta OCD\)和\(\Delta ABC\)是等边三角形,可证\(\Delta BOC \cong \Delta ADC\),进而得\(\angle BOC = \angle ADC\),所以\(\angle ADO = \angle ADC - \angle ODC = 150^\circ - 60^\circ = 90^\circ \),\(\Delta ADO\)是直角三角形。
第182题
探究:当α为___°时,△AOD是等腰三角形。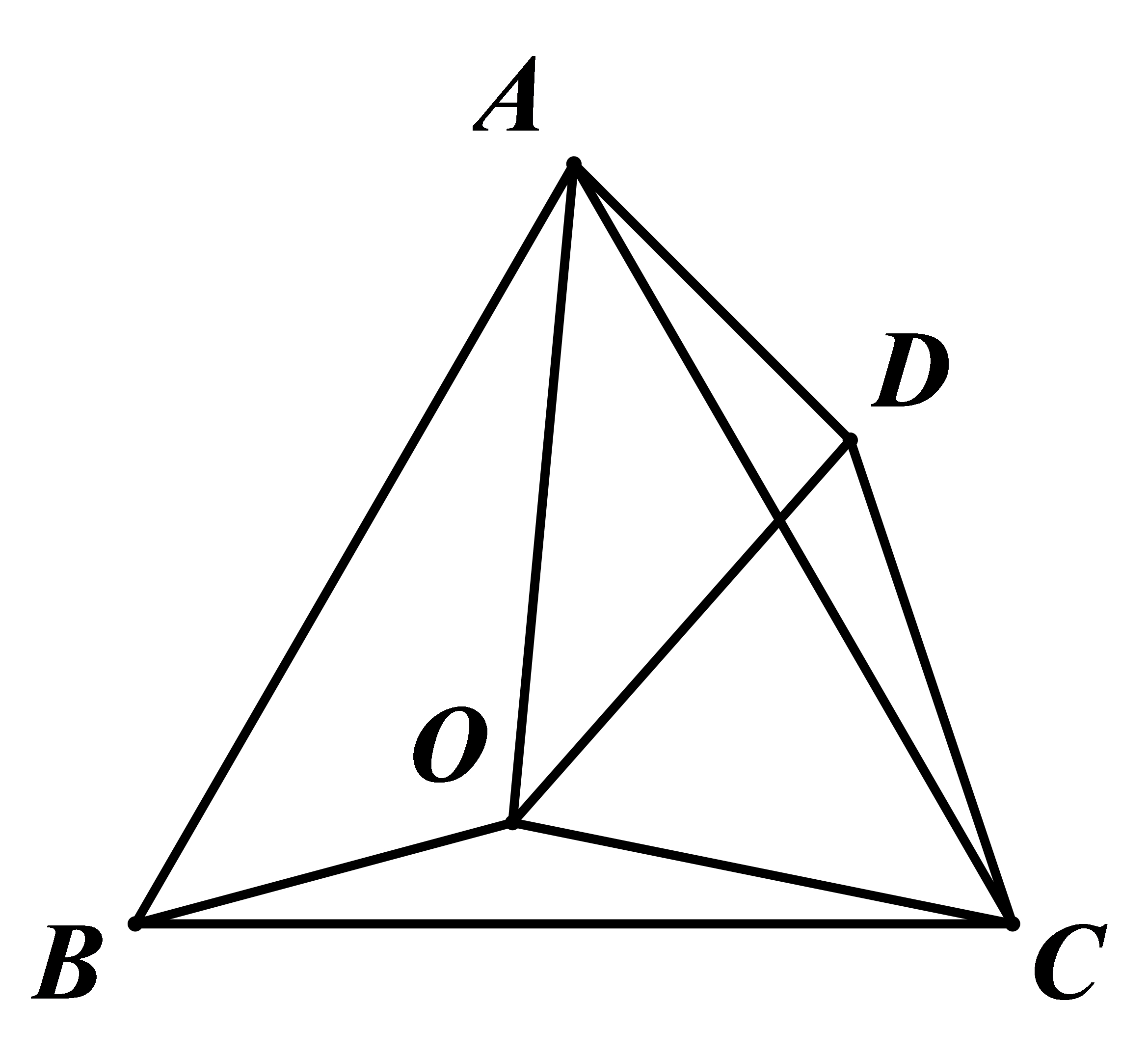
参考答案:当\(\alpha \)为\(110^\circ \),\(125^\circ \),\(140^\circ \)时,\(\Delta ADO\)是等腰三角形。
第183题
如图,点D为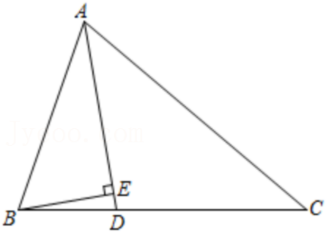
A.2
B.3
C.4
D.5
参考答案:B
第187题
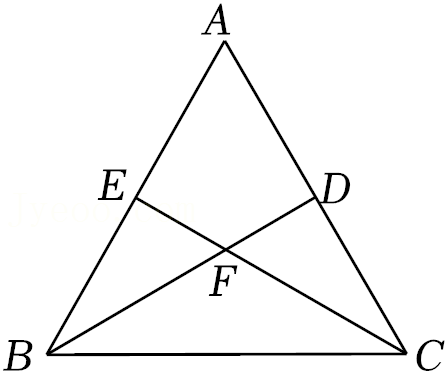
如图,△ABC是等边三角形,AE=BD,AD与CE交于点F。求∠CFD的度数。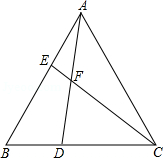
参考答案:\(\because \Delta ABC\)是等边三角形\(\therefore AB = CA\),\(\angle B = \angle CAB = 60^\circ \)\(\therefore \Delta ABD \cong \Delta CAE\)\(\therefore \angle BAD = \angle ACE\)\(\because \angle BAD + \angle DAC = \angle BAC = 60^\circ \)\(\therefore \angle ACE + \angle DAC = 60^\circ \)\(\because \angle DFC = \angle ACE + \angle DAC\)\(\therefore \angle DFC = 60^\circ \)。
第189题
已知∠AOB=30°,点P在∠AOB的内部,P1与P关于OA对称,P2与P关于OB对称, 判定
参考答案:\(\because {P_1}\)与\(P\)关于\(OB\)对称\(\therefore OP = O{P_1}\),\(\angle {P_1}OB = BOP\)\(\because {P_2}\)与\(P\)关于\(OA\)对称\(\therefore OP = O{P_2}\),\(\angle {P_2}OA = AOP\)\(\therefore O{P_1} = O{P_2}\),\(\angle {P_1}O{P_2} = 2\angle BOA = 60^\circ \)\(\therefore \)△\({P_1}O{P_2}\)为等边三角形
第191题
如图,等边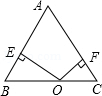
A.2
B.\(2\sqrt 3 \)
C.4
D.\(4\sqrt 3 \)
参考答案:C
第197题
下列命题错误的是( )
A.有两个内角分别是70°、40°的三角形是等腰三角形。
B.平行于等腰三角形一边的直线所截得的三角形仍是等腰三角形。
C.有两个内角不等的三角形不是等腰三角形。
D.如果一个三角形有不在同一顶点处的两个外角相等,那么这个三角形是等腰三角形。
参考答案:C