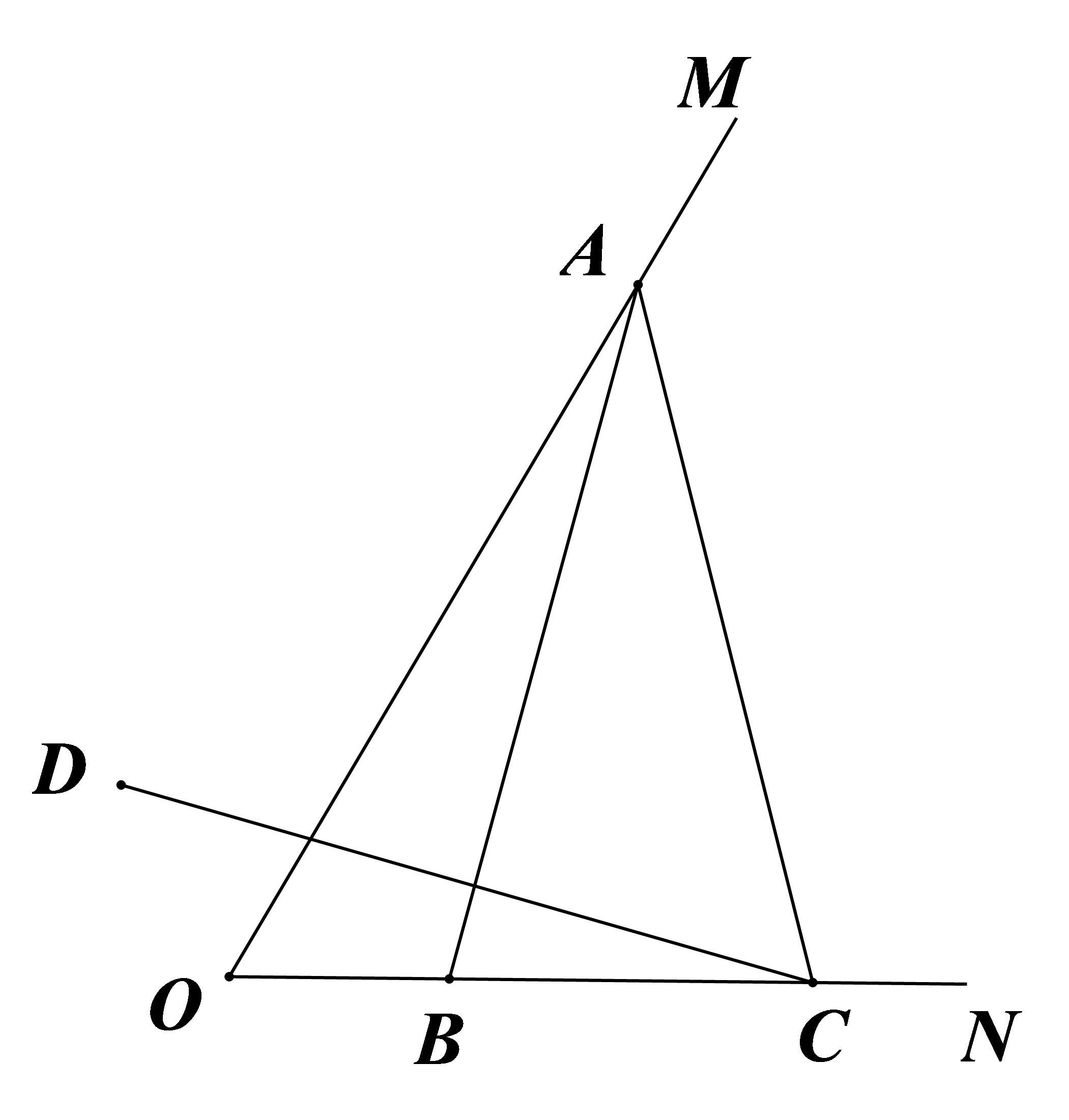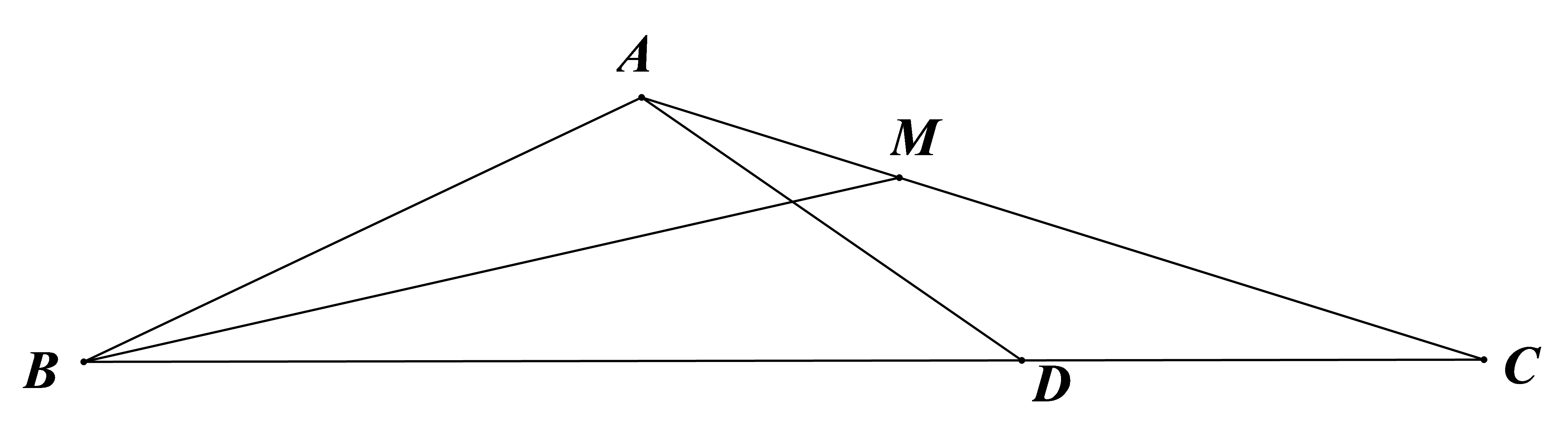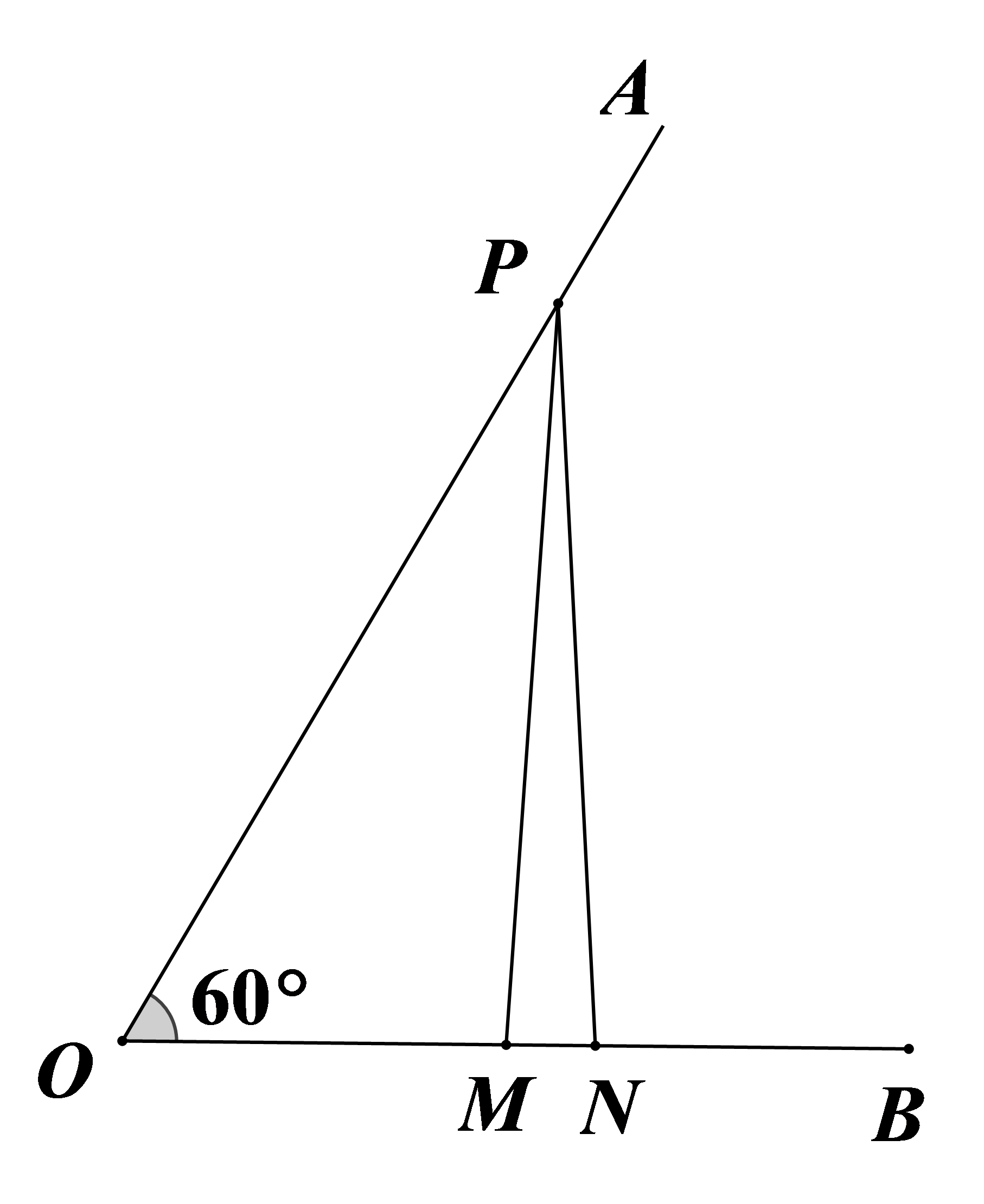第241题

如图，∠MON=60°，点A在射线OM上，点B，C在射线ON上（点C在点B的右侧），且∠OAB+∠OAC=60°.点B关于直线OM的对称点为D，连接CD．用等式表示线段CD，AB之间的数量关系，并证明。

参考答案：\(CD = AB\)证明：连接\(AD\)，\(OD\)，\(\because \)点\(B\)关于直线\(OM\)的对称点为\(D\)，点\(A\)在射线\(OM\)上，\(\therefore AD = AB\)，\(\angle OAD = \angle OAB\)，\(\because \angle OAB + \angle OAC = 60^\circ \)，\(\therefore \angle OAD + \angle OAC = 60^\circ \)，即\(\angle DAC = 60^\circ \)，在\(\vartriangle OAC\)中，\(\angle ACO = 180^\circ - \angle OAC - \angle AOC = 180^\circ - (60^\circ - \angle OAB) - 60^\circ = 60^\circ + \angle OAB\)，又\(\because \angle ABC = \angle AOB + \angle OAB = 60^\circ + \angle OAB\)，\(\therefore \angle ACO = \angle ABC\)，\(\therefore AB = AC\)，\(\therefore AC = AD\)，又\(\because \angle CAD = 60^\circ \)，\(\therefore \vartriangle ACD\)是等边三角形，\(\therefore CD = AD\)，\(\therefore CD = AB\)．

第242题

求∠AEC的度数；

参考答案：60°

第243题

当\(0^\circ < \alpha < 60^\circ \)时，用等式表示线段AE，CD，DE之间的数量关系，并证明。

参考答案：

第244题

如图，在△ABC中，AB=BC=3，∠BAC=30°，分别以点A，C为圆心，AC长为半径作弧，两弧交于点D，连接DA，DC，BD交AC于点O，下面结论中，①AD=CD；②BD⊥AC；③AC=6，正确的是___。（填序号）

参考答案：①②

第245题

如图，等边三角形ABC的三个顶点都在坐标轴上，A(—1,0)，过点B作BD⊥AB，BD交x轴于点D，则点D的坐标为___。

参考答案：（3,0）

第246题

如图，BM是\(△ABC\)的角平分线，D是BC边上一点，连接AD，使AD=DC，且∠BAD=120°，则∠AMB为___。

参考答案：30°

第247题

如图，∠ABC=60°，AB=3，动点P从点B出发，以1cm/s的速度沿射线BC运动，设点P的运动时间为t秒，当△ABP是钝角三角形时，t的取值范围是___。

参考答案：\(0 < t < 1.5或t > 6\)

第248题

如图，在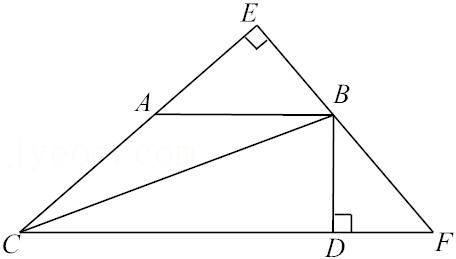\(△ABC\)中，AB=AC，AB∥CD，过点B作BF⊥AC交CA延长线于E，交CD延长线于点F，BD⊥CD，CD=8，BD=3，BF=4，则\(△ABE\)的周长为___。

参考答案：11

第249题

如图，∠AOB=60°，点P在射线OA上，OP=10，点M、N在射线OB上，PM=PN，若MN=2，则OM的长度为___。

参考答案：4

第250题

\( (ab{)}^{5}\)；

参考答案：\( {a}^{5}{b}^{5}\)

第251题

\({( - 4{x^3})^2}\)；

参考答案：\( 16{x}^{6}\)

第252题

\( {\left(-3x\right)}^{3}\)。

参考答案：\( -27{x}^{3}\)

第253题

计算：\({0.75^{2022}} \times {( - \frac{4}{3})^{2021}}\)的结果为\((\)　　\()\)

A.\(\frac{4}{3}\)

B.\(\frac{3}{4}\)

C.\( - \frac{4}{3}\)

D.\( - \frac{3}{4}\)

参考答案：D

第254题

\( {\left(-4\times 1{0}^{3}\right)}^{2}\)；            

参考答案：\( 1.6\times 1{0}^{7}\)

第255题

\( (5a+4b)\left(5a-4b-3\right)\) 。

参考答案：8

第256题

下列运算正确的是\((\)　　\()\)

A.\({(ab)^2} = {a^2}{b^2}\)

B.\({a^3} + {a^2} = {a^5}\)

C.\({a^3} \cdot {a^2} = {a^6}\)

D.\( (a+b{)}^{2}={a}^{2}+{b}^{2}\)

参考答案：A

第257题

已知\( {2}^{n}=a\)，\( {3}^{n}=b\)，求\( {6}^{n}\)的值。

参考答案：\( ab\)

第258题

已知\( {x}^{n}=5\)，\( {y}^{n}=3\)，求\( ({x}^{2}y{)}^{2n}\)的值。

参考答案：5625

第259题

计算： \( -{a}^{2}\cdot {a}^{4}+(-2{a}^{3}{)}^{2}-(-3{a}^{2}{)}^{3}\) 。

参考答案：\( 30{a}^{6}\)

第260题

\( {\left(-{x}^{3}\right)}^{2}\cdot {\left(-{x}^{2}\right)}^{3}\)               

参考答案：\( -{x}^{12}\)