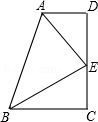
解:
①②③\( \Rightarrow AD//BC\):
\(\because \)\(AE \bot EB\)
\(\therefore \angle EAB + \angle EBA = 90^\circ \)
\(\because \)\(AE\)平分\(\angle BAD\),\(BE\)平分\(\angle ABC\)
\(\therefore \angle EAB = \frac{1}{2}\angle DAB\),\(\angle EBA = \frac{1}{2}\angle CBA\)
\(\therefore \angle DAB + \angle CBA = 180^\circ \)
\(\therefore AD//BC\)
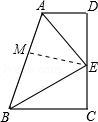
①②④\( \Rightarrow AD//BC\):
在\(AB\)上取点\(M\),使\(AM = AD\),连接\(EM\)
又\(\because AB = AD + BC\),
\(\therefore MB = BC\)
在\(\Delta AEM\)和\(\Delta AED\)中
\(\begin{cases}
AM = AD \\\
\angle MAE = \angle DAE \\\
AE = AE \\\
\end{cases}\)
\(\therefore \Delta AEM \cong \Delta AED(SAS)\)
\(\therefore \angle D = \angle AME\)
在\(\Delta BEM\)和\(\Delta BEC\)中
\(\begin{cases}
BM = BC \\\
\angle MBE = \angle CBE \\\
BE = BE \\\
\end{cases}\)
\(\therefore \Delta BEM \cong \Delta BEC(SAS)\)
\(\therefore \angle C = \angle BME\)
\(\therefore \)\(\angle D + \angle C = \angle AME + \angle BME = 180^\circ \)
\(\therefore AD//BC\).
①③④和②③④都不能推出\(AD//BC\).