“微信扫一扫”进入考试题库练习及模拟考试
初中数学八年级上册试题库(555题)
A.\(\frac{3}{2}\)
B.3
C.6
D.12
参考答案:B
A.角的内部到角的两边的距离相等的点在角的平分线上
B.角平分线上的点到这个角两边的距离相等
C.三角形三条角平分线的交点到三条边的距离相等
D.以上均不正确
参考答案:A
A.2
B.3
C.4
D.5
参考答案:C
第104题
在正方形网格中,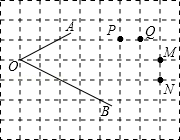
A.点\(M\)
B.点\(N\)
C.点\(P\)
D.点\(Q\)
参考答案:A
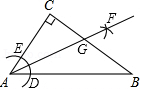
第105题
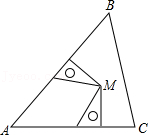
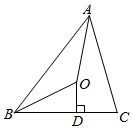
如图,在四边形
参考答案:
过点
在
{\angle GCE = \angle B} \\
{CE = EB} \\
{\angle CEG = \angle BEH}
\end{array}} \right.\)
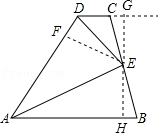
第106题
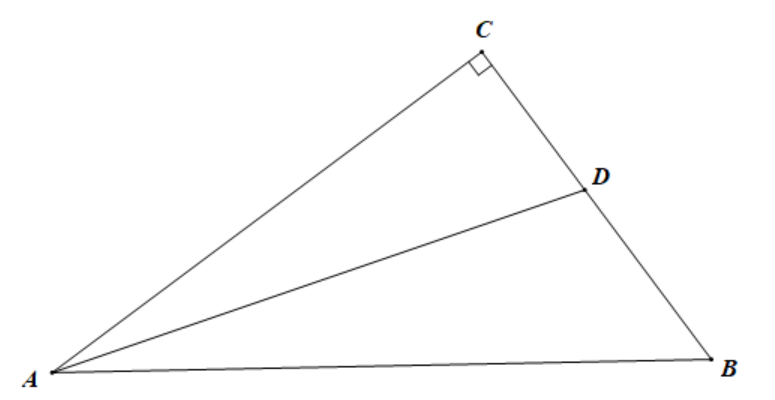
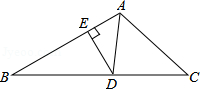
如图:已知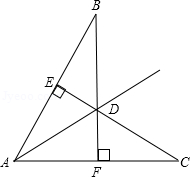
参考答案:\(\because BF \bot AC\),\(CE \bot AB\),\(\therefore \angle BED = \angle CFD = 90^\circ \),在\(\Delta BED\)和\(\Delta CFD\)中,\(\left\{ {\begin{array}{*{20}{l}}
{\angle BED = \angle CFD} \\
{\angle BDE = \angle CDF} \\
{BD = CD}
\end{array}} \right.\),\(\therefore \Delta BED \cong \Delta CFD(AAS)\),\(\therefore DE = DF\),又\(\because DE \bot AB\),\(DF \bot AC\),\(\therefore \)点\(D\)在\(\angle BAC\)的平分线上.
第107题
如图,直线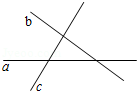
A.一处
B.两处
C.三处
D.四处
参考答案:D
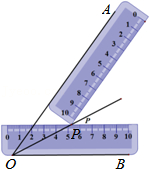
第108题
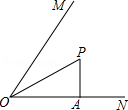
点
A.\(PQ < 5\)
B.\(PQ > 5\)
C.\(PQ⩾5\)
D.\(PQ⩽5\)
参考答案:D
A.等于3
B.大于3
C.小于3
D.无法确定
参考答案:A
A.3
B.10
C.15
D.30
参考答案:C
参考答案:过点
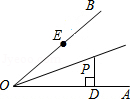
第112题
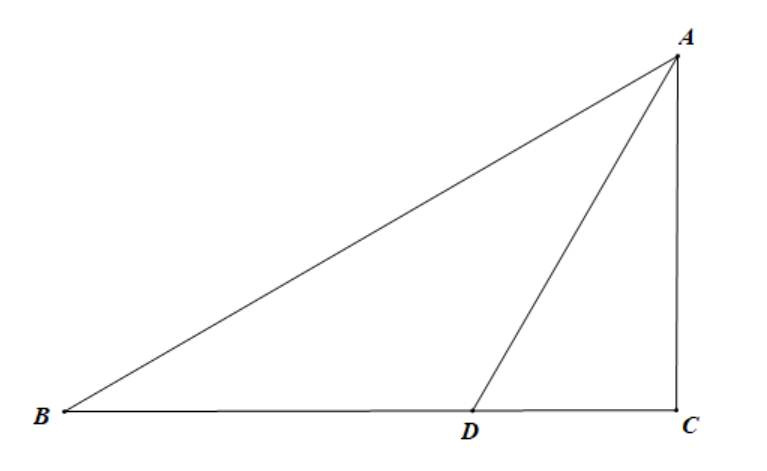
如图,
参考答案:如图,过点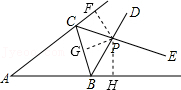
A.1
B.2
C.3
D.4
参考答案:B
A.\(\angle A\)的平分线上
B.\(AC\)边的高上
C.\(BC\)边的垂直平分线上
D.\(AB\)边的中线上
参考答案:A
A.\(5cm\)
B.\(4cm\)
C.\(3cm\)
D.\(2cm\)
参考答案:B
A.20
B.30
C.50
D.100
参考答案:C
参考答案:12
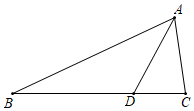
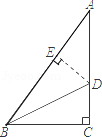
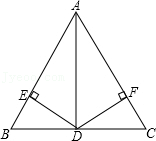
参考答案:\(\because AD\)平分\(\angle BAC\),\(DE \bot AB\),\(DF \bot AC\),\(\therefore DE = DF\),\(\angle BED = \angle CFD = 90^\circ \),\(\because D\)是\(BC\)的中点,\(\therefore BD = CD\)在\({\rm{Rt}}\Delta {\rm{BDE}}\)和\({\rm{Rt}}\Delta {\rm{CDF}}\)中\(\because DE = DF\),\(DB = DC\),\(\therefore {\rm{Rt}}\Delta {\rm{BDE}} \cong {\rm{Rt}}\Delta {\rm{CDF}}({\rm{HL}})\)\(\therefore \angle B = \angle C\)。
A.3
B.4
C.6
D.5
参考答案:D
A.14
B.8
C.16
D.6
参考答案:B