“微信扫一扫”进入考试题库练习及模拟考试
初中数学八年级上册试题库(555题)
A.只有①③
B.只有①③④
C.只有②④
D.①②③④
参考答案:B
第48题
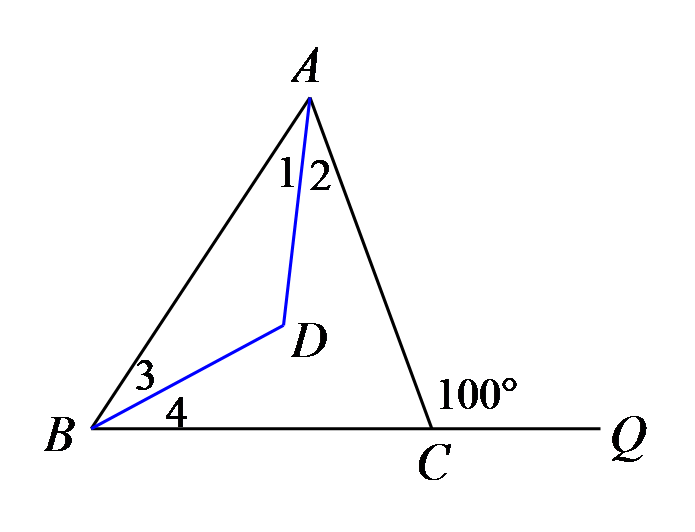
如图,在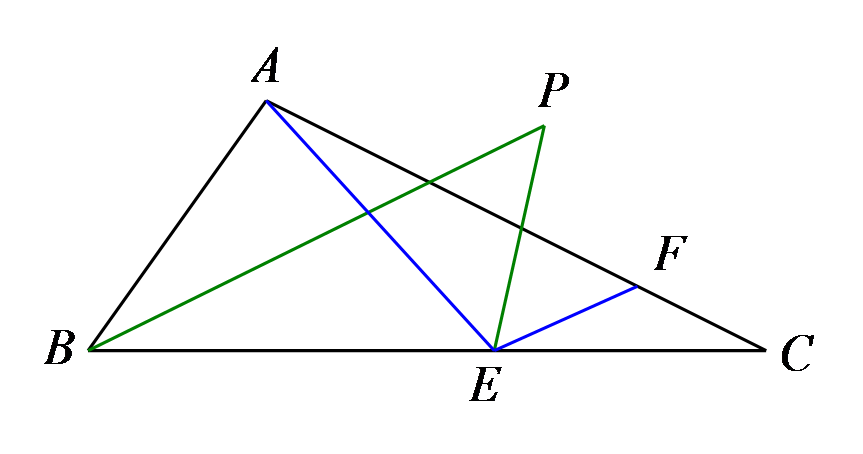
参考答案:56°
第50题
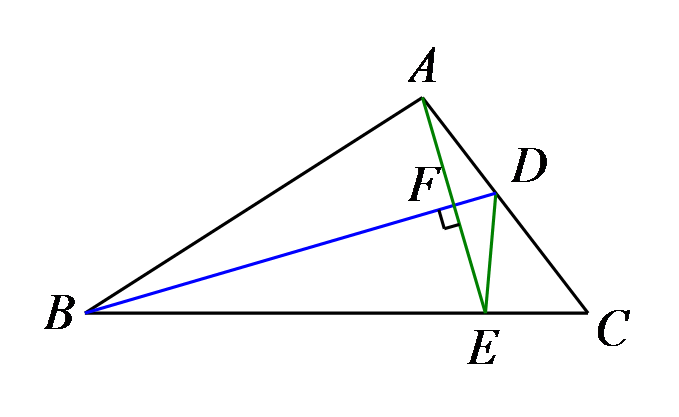
求∠EAD的度数。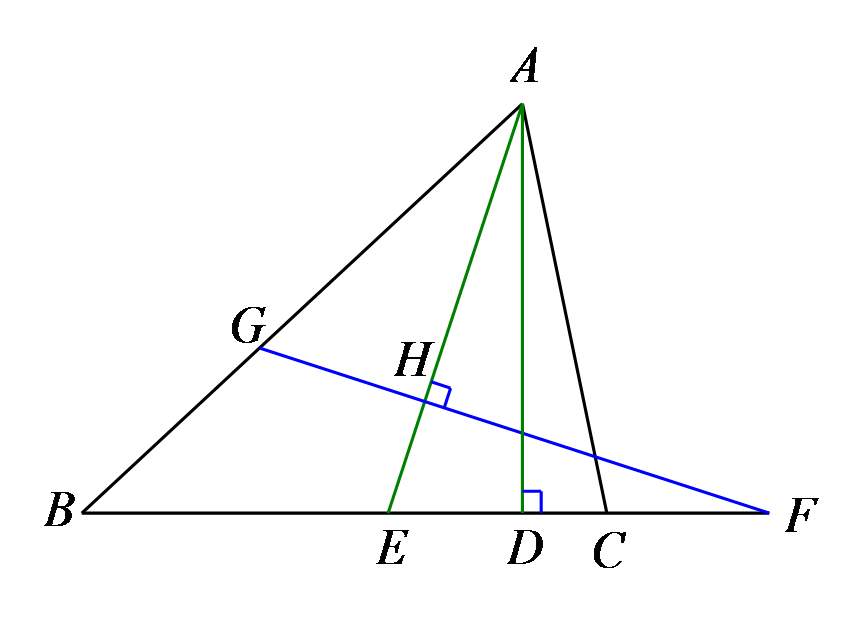
参考答案:20°(1)\(\because \angle B = 40^\circ \),\(\angle ACB = 80^\circ \),\(\therefore \angle BAC = 180^\circ - 40^\circ - 80^\circ = 60^\circ \),\(\because AE\)是\(\Delta ABC\)的角平分线,\(\therefore \angle BAE = \frac{1}{2}\angle BAC = 30^\circ \),\(\because FG \bot AE\),\(\therefore \angle AHG = 90^\circ \),\(\therefore \angle AGF = 180^\circ - 90^\circ - 30^\circ = 60^\circ \);(2)\(\because AD\)是\(\Delta ABC\)的高,\(\therefore \angle ADC = 90^\circ \),\(\because \angle ACB = 80^\circ \),\(\therefore \angle CAD = 180^\circ - 90^\circ - 80^\circ = 10^\circ \),\(\because \angle BAC = 60^\circ \),\(AE\)是\(\Delta ABC\)的角平分线,\(\therefore \angle CAE = \frac{1}{2}\angle BAC = 30^\circ \),\(\therefore \angle EAD = \angle CAE - \angle CAD = 30^\circ - 10^\circ = 20^\circ \).
第52题
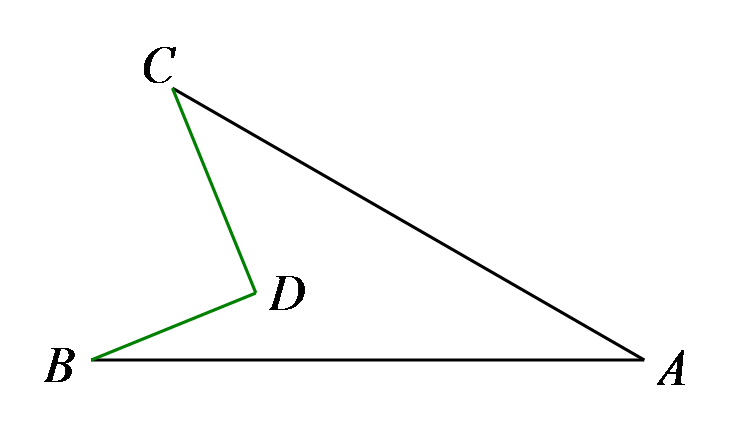
如图2,若∠ABC=α,∠BDA=β,求∠FAD+∠C的度数(用含α和β的代数式表示)。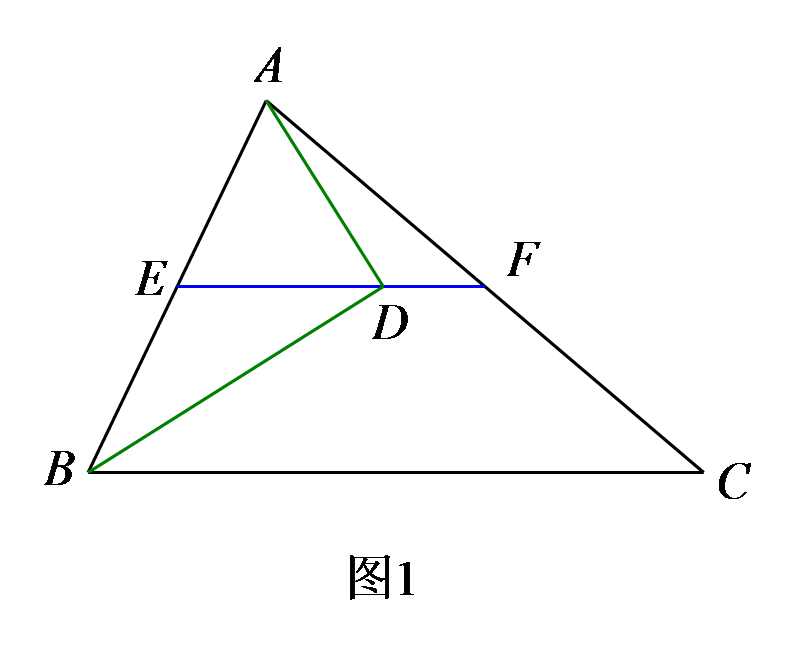
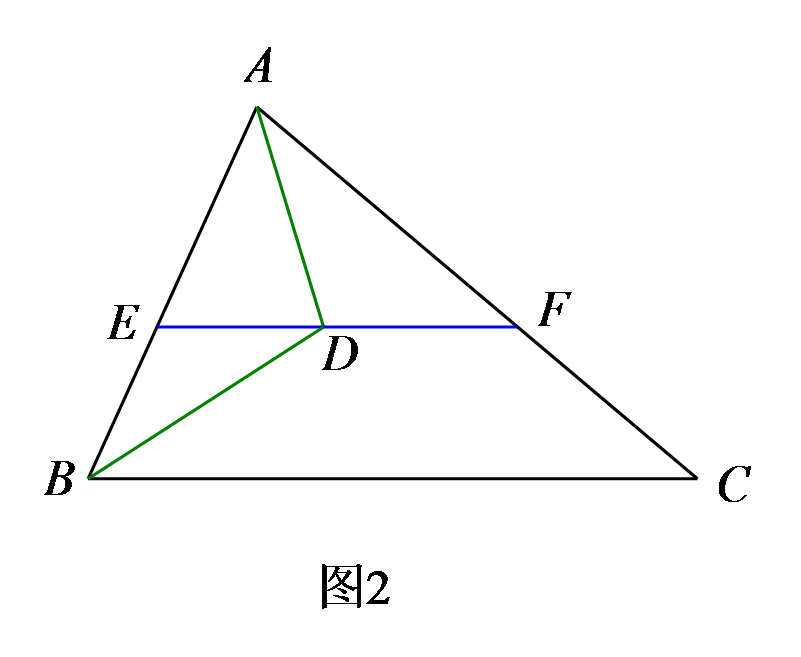
参考答案:
β-0.2α
(1)
又
又
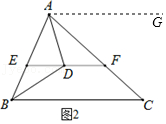
(2)如图2,过点
则
则
第54题
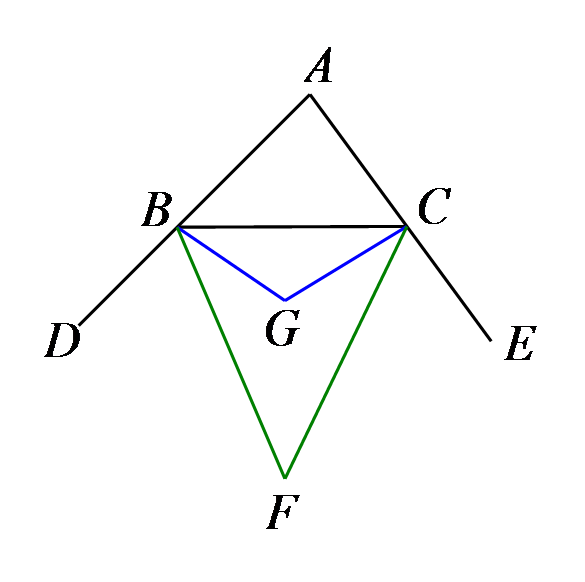
如图2,当点F在AE的延长线上时,请猜想∠EFD与∠B,∠C之间的数量关系,并加以证明。
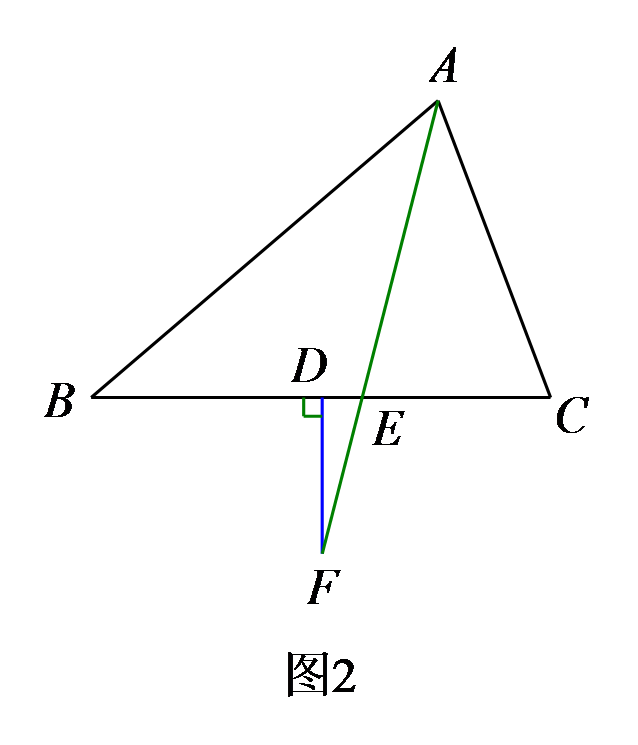
参考答案:\(\angle EFD = \frac{1}{2}(\angle C - \angle B)\)(1)\(\because AE\)平分\(\angle BAC\),\(\therefore \)\(\angle BAE = \frac{1}{2}\angle BAC = \frac{1}{2}(180^\circ - \angle B - \angle C) = 90^\circ - \frac{1}{2}(\angle B + \angle C)\),\(\because \angle FEC = \angle B + \angle BAE\),则\(\angle FEC = \angle B + 90^\circ - \frac{1}{2}(\angle B + \angle C) = 90^\circ + \frac{1}{2}(\angle B - \angle C)\),\(\because FD \bot EC\),\(\therefore \angle EFD = 90^\circ - \angle FEC\),则\(\angle EFD = 90^\circ - [90^\circ + 2(\angle B - \angle C)] = \frac{1}{2}(\angle C - \angle B)\),\(\because \angle B = 40^\circ \),\(\angle C = 60^\circ \),\(\therefore \angle EFD = \frac{1}{2}(60 - 40) = 10^\circ \);(2)猜想:\(\angle EFD = \frac{1}{2}(\angle C - \angle B)\).证明:同(1)可证:\(\angle AEC = 90^\circ + \frac{1}{2}(\angle B - \angle C)\),\(\therefore \angle DEF = \angle AEC = 90^\circ + 2(\angle B - \angle C)\),\(\therefore \)\(\angle EFD = 90^\circ - [90^\circ + \frac{1}{2}(\angle B - \angle C)] = \frac{1}{2}(\angle C - \angle B)\).