“微信扫一扫”进入考试题库练习及模拟考试
初中数学八年级上册试题库(555题)
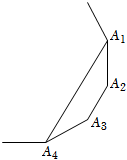
第68题
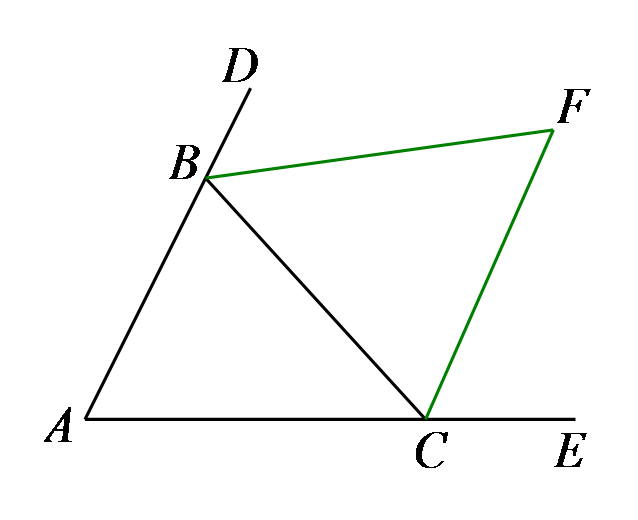
如图,把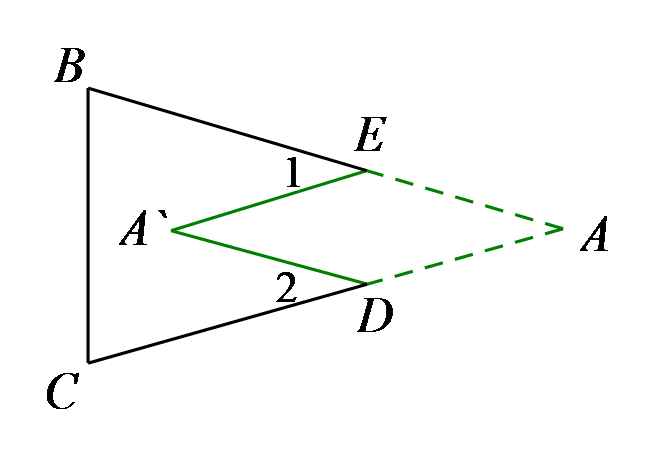
A.∠A=∠1+∠2
B.2∠A=∠1+∠2
C.3∠A=2∠1+∠2
D.3∠A=2(∠1+∠2)
参考答案:B
A.①②③
B.①③④
C.①④
D.①②④
参考答案:C
第70题
如图,在
A.40°
B.20°
C.55°
D.30°
参考答案:A
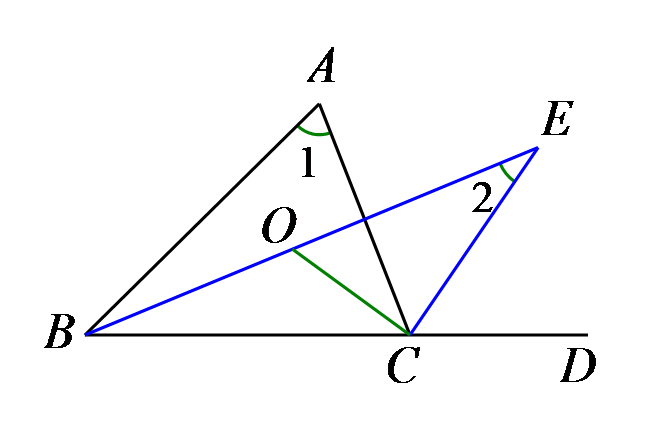
第71题
如图,在△ABC中,∠A=20°,CD是∠BCA的平分线,△CDA中,DE是CA边上的高,又有∠EDA=∠CDB,求∠B的大小。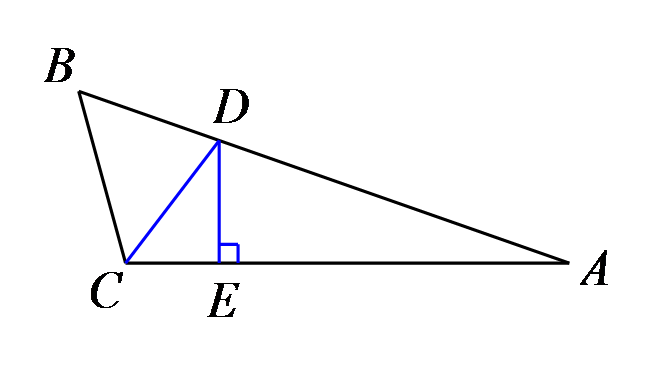
参考答案:60°。∵DE是CA边上的高,∴∠DEA=∠DEC=90°.∵∠A=20°,∴∠EDA=90°-20°=70°.∵∠EDA=∠CDB,∴∠CDE=180°-70°×2=40°.在Rt△CDE中,∠DCE=90°-40°=50°.∵CD是∠BCA的平分线,∴∠BCA=2∠DCE=2×50°=100°.∴∠B=180°-∠BCA-∠A=60°.
第75题
如图,在△ABC中,点M、N是∠ABC与∠ACB三等分线的交点,若∠A=60°,求∠BMN的度数。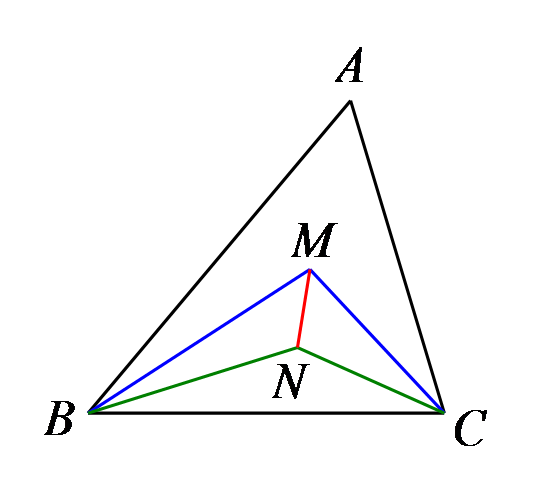
参考答案:见解析
解析:
50°。
如图,过点N作NG⊥BC于G,NE⊥BM于E,NF⊥CM于F,
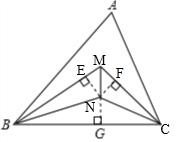
∵∠ABC的三等分线与∠ACB的三等分线分别交于点M、N,
∴BN平分∠MBC,CN平分∠MCB,
∴NE=NG,NF=NG,
∴NE=NF,
∴MN平分∠BMC,
∴∠BMN=
∵∠A=60°,
∴∠ABC+∠ACB=180°−∠A=180°−60°=120°,
根据三等分,∠MBC+∠MCB=
在△BMC中,∠BMC=180°−(∠MBC+∠MCB)=180°−80°=100°
∴∠BMN=
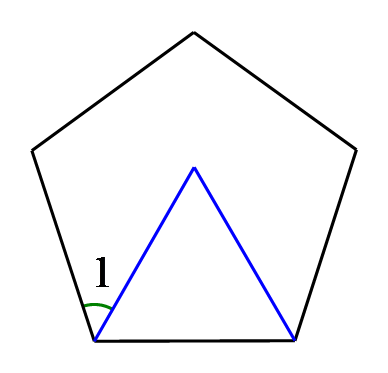
第80题
要使五边形木架不变形,至少要再钉上几根木条?如果是七边形呢?如果是n边形呢?
参考答案:2;4;\(n - 3\)
解:除选定的一个顶点外,相邻的两个顶点也排除,这样可以连接对角线的顶点只有\(n - 3\)个。