如图，线段\(AC\)、\(BD\)相交于点\(E\)，连接\(AB\)、\(CD\)，已知\(\angle A = \angle D = 90^\circ \

“微信扫一扫”进入题库练习及模拟考试

初中数学八年级上册试题库（555题）

如图，线段\(AC\)、\(BD\)相交于点\(E\)，连接\(AB\)、\(CD\)，已知\(\angle A = \angle D = 90^\circ \)，\(AC = BD\)，

求证：\(BE = CE\)。

知识点：第十二章　全等三角形

参考答案：

证明：连接\(BC\)，如图所示：

\(\because \angle A = \angle D = 90^\circ \)，

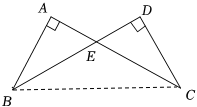
在\({\rm{Rt}}\Delta {\rm{ABC}}\)和\({\rm{Rt}}\Delta {\rm{DCB}}\)中，

\(\left\{ {\begin{array}{*{20}{l}}
{AC = BD} \\
{BC = CB}
\end{array}} \right.\)，

\(\therefore {\rm{Rt}}\Delta ABC \cong {\rm{Rt}}\Delta DCB(HL)\)，

\(\therefore AB = DC\)，

在\(\Delta ABE\)和\(\Delta DCE\)中，

\(\left\{ {\begin{array}{*{20}{l}}
\begin{gathered}
\angle A = \angle D \\
\angle AEB = \angle DEC \\
\end{gathered} \\
{AB = DC}
\end{array}} \right.\)，

\(\therefore \Delta ABE \cong \Delta DCE(AAS)\)，

\(\therefore BE = CE\)。

声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2022/7/17 15:34:21；用户：邓芸；邮箱：syxx019@xyh.com；学号：21059015

进入考试题库

初中数学八年级上册试题库（555题）

知识点：第十二章 全等三角形

知识点：第十二章　全等三角形