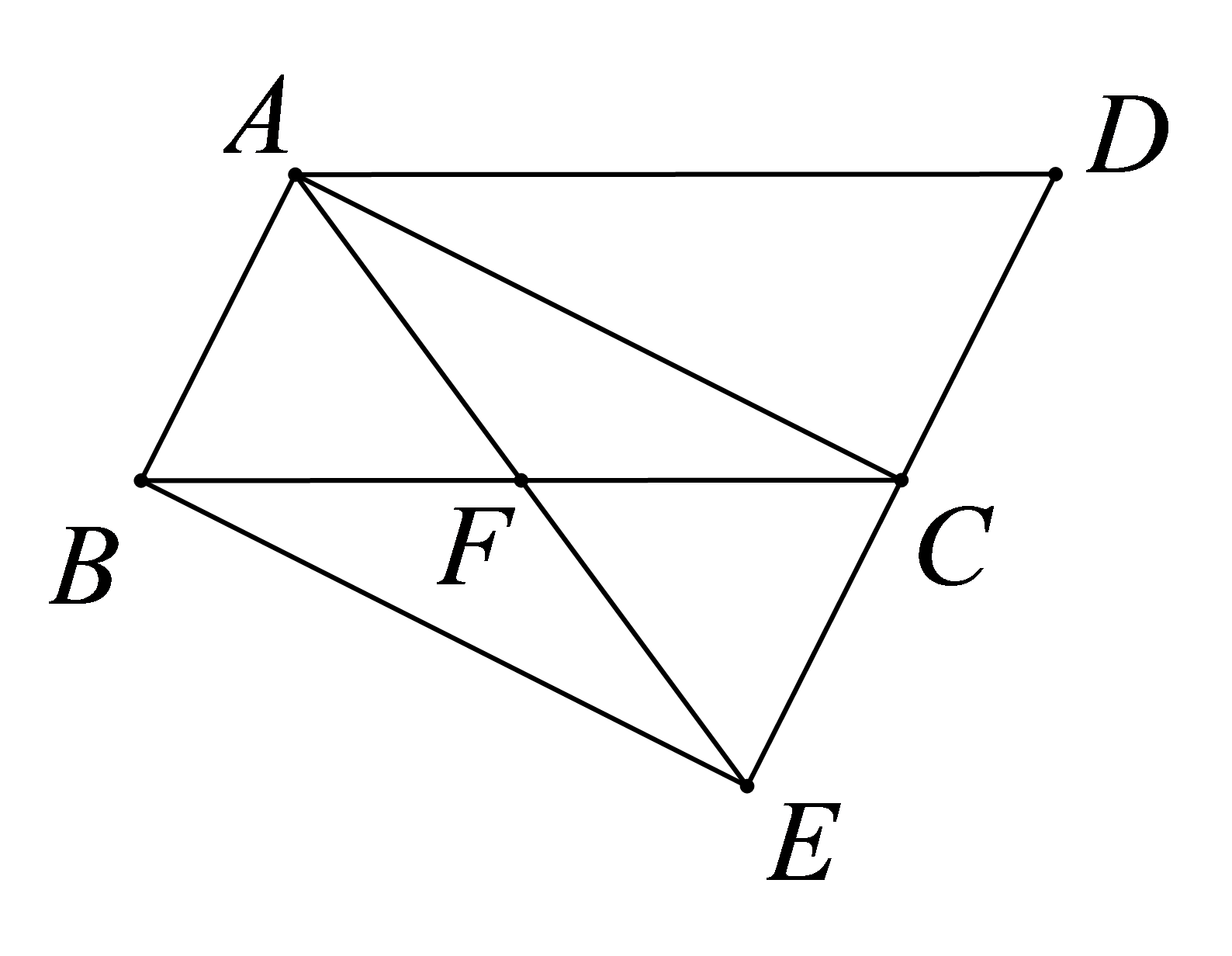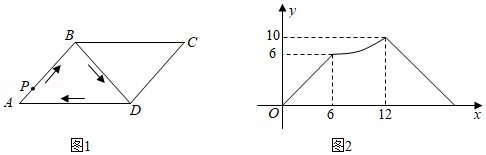“微信扫一扫”进入考试题库练习及模拟考试
初中数学八年级下册(648题)
第601题 当\(\angle BAD = 100^\circ \)时,求\(\angle EAF\)的度数。
参考答案:解:
\(\because \)四边形\(ABCD\)是菱形,
\(\therefore AD//BC\),
\(\therefore \angle BAD + \angle B = 180^\circ \),
\(\because \angle BAD = 100^\circ \),
\(\therefore \angle B = 80^\circ \)
\(\because AE \bot BC\),
\(\therefore \angle AEB = 90^\circ \),
\(\therefore \angle BAE = 10^\circ \),
\(\therefore \angle DAF = 10^\circ \),
\(\therefore \angle EAF = \angle BAD - \angle BAE - \angle DAF \)
\(= 100^\circ - 10^\circ - 10^\circ = 80^\circ \)。
参考答案:证明:
\(\because \)四边形\(ABCD\)是平行四边形,
\(\therefore AB = CD\),
\(AB//CD\),
\(\angle ABC = \angle D\),
\(\because CE = CD\),
\(\therefore AB = CE\),
\(\therefore \)四边形\(ABEC\)是平行四边形,
\(\therefore BC = 2BF\),\(AE = 2AF\),
\(\because \angle AFC \)
\(= \angle ABC + \angle BAE = 2\angle D\),
\(\therefore \angle ABC = \angle BAE\),
\(\therefore AF = BF\),
\(\therefore AE = BC\),
\(\therefore \)四边形\(ABEC\)是矩形。
参考答案:证明:\(\because \)点\(E\),\(G\)分别是\(AD\),\(BD\)的中点,
\(\therefore EG//AB\),\(EG = \frac{1}{2}AB\)
∵点\(H,F\)分别是\(AC,BC\)的中点,
∴\(HF//AB\),\(HF = \frac{1}{2}AB\)
\(\therefore EG//HF\),\(EG = HF\)
\(\therefore \)四边形\(EHFG\)是平行四边形.
∵点\(H,E\)分别是\(AC,AD\)的中点,
∴\(EH = \frac{1}{2}CD\)
\(\because AB = CD\),
\(\therefore EG = EH\),
\(\therefore \)四边形\(EHFG\)是菱形。
第605题 求证:四边形\(ABCD\)是正方形。
参考答案:
作
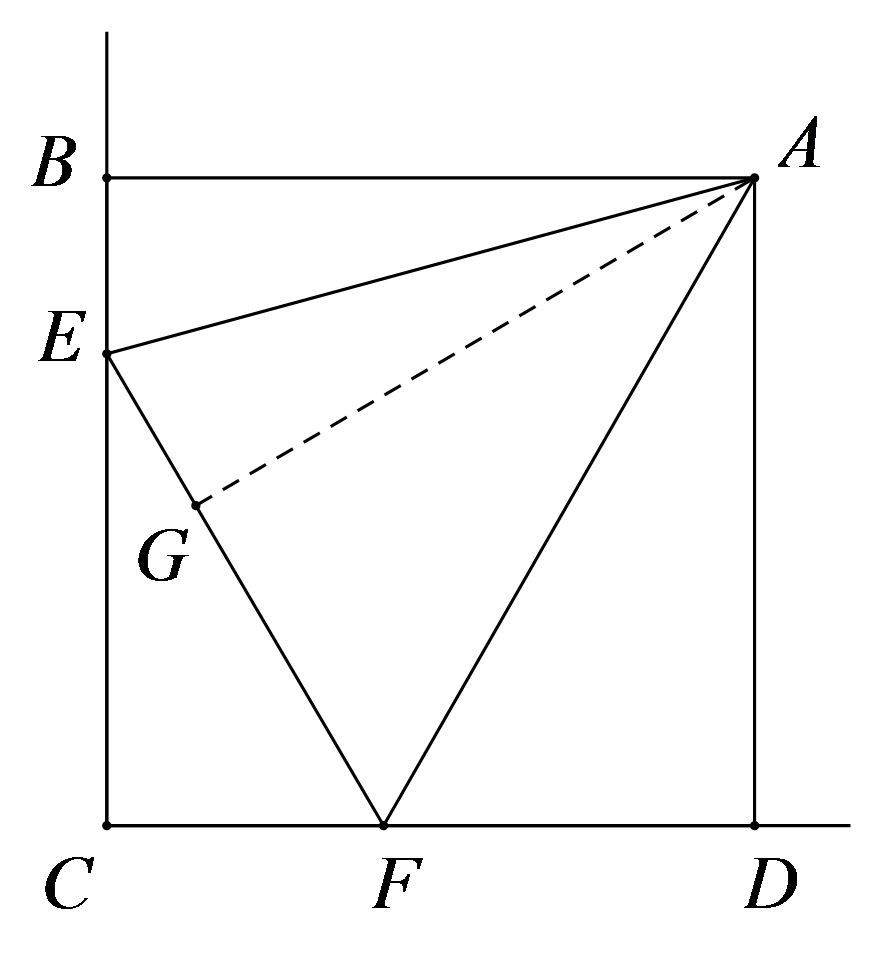
则
第606题
求证:四边形
参考答案:
证明: ∵
∴四边形
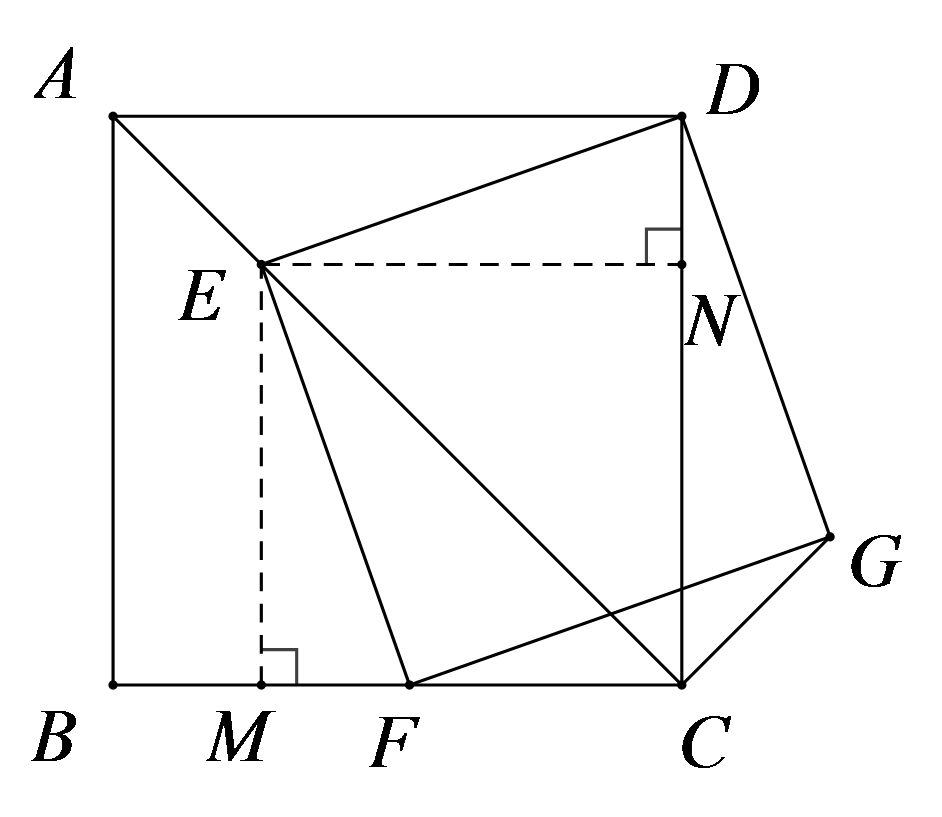
如图,作
在
第607题
探究:\(CE\)与\(CG\)有怎样的位置关系?请说明理由。
参考答案:\(CE \bot CG\),
理由如下:
\(\because \)正方形\(DEFG\)和正方形\(ABCD\),
\(\therefore DE = DG\),\(AD = DC\),
\(\because \angle CDG + \angle CDE \)
\(= \angle ADE + \angle CDE = 90^\circ \),
\(\therefore \angle CDG = \angle ADE\),
在\(\Delta ADE\)和\(\Delta CDG\)中,
\(\left\{ {\begin{array}{*{20}{l}}
{AD = CD} \\
{\angle ADE = \angle CDG} \\
{DE = DG}
\end{array}} \right.\),
\(\therefore \Delta ADE \cong \Delta CDG(SAS)\),
\(\therefore \angle CDA = \angle DCG\),
\(\because \angle ACD + \angle CAD + \angle ADC = 180^\circ \),
\(\angle ADC = 90^\circ \),
\(\therefore \angle ACG = \angle ACD + \angle DCG \)
\(= \angle ACD + \angle CAD = 90^\circ \),
\(\therefore CE \bot CG\)。
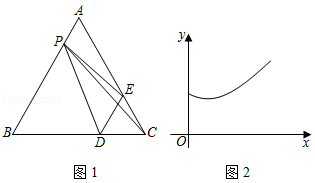
A.线段\(PE\)
B.线段\(PC\)
C.线段\(PD\)
D.线段\(DE\)
参考答案:C
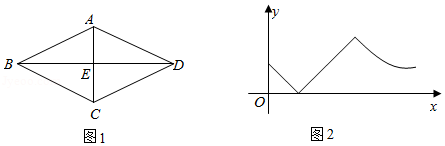
A.\(C \to B \to A \to E\)
B.\(C \to D \to E \to A\)
C.\(A \to E \to C \to B\)
D.\(A \to E \to D \to C\)
参考答案:D
第610题
按如图所示的运算程序,能使输出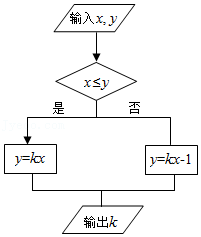
A.\(x = 1\),\(y = 0\)
B.\(x = 2\),\(y = 1\)
C.\(x = 1\),\(y = 3\)
D.\(x = 2\),\(y = 3\)
参考答案:C
A.\(24\sqrt 5 \)
B.\(10\sqrt {11} \)
C.\(12\sqrt 5 \)
D.36
参考答案:B
第612题
在同一坐标系中,若直线
A.\(k < 0\),\(b < 0\)
B.\(k < 0\),\(b > 0\)
C.\(k > 0\),\(b < 0\)
D.\(k > 0\),\(b > 0\)
参考答案:D
A.线段\(EC\)
B.线段\(AE\)
C.线段\(EF\)
D.线段\(BF\)
参考答案:B
A.\(b \leqslant - 1\)或\(b \geqslant 3\)
B.\( - 1 \leqslant b \leqslant 3\)
C.\(b \leqslant 1\)或\(b \geqslant 5\)
D.\(1 \leqslant b \leqslant 5\)
参考答案:D
参考答案:\(x < 5且x \ne - 7\);
\(\sqrt 2 - 3\)
参考答案:\(0 < k < 3\)
第619题
已知一次函数
参考答案:\(\sqrt {13} \)
第620题
在平面直角坐标系
参考答案:\(1 < n < 7\)