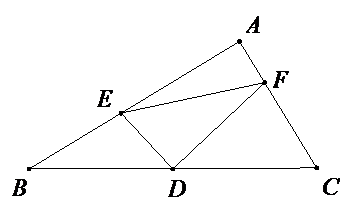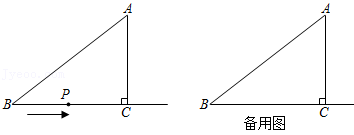“微信扫一扫”进入考试题库练习及模拟考试
初中数学八年级下册(648题)
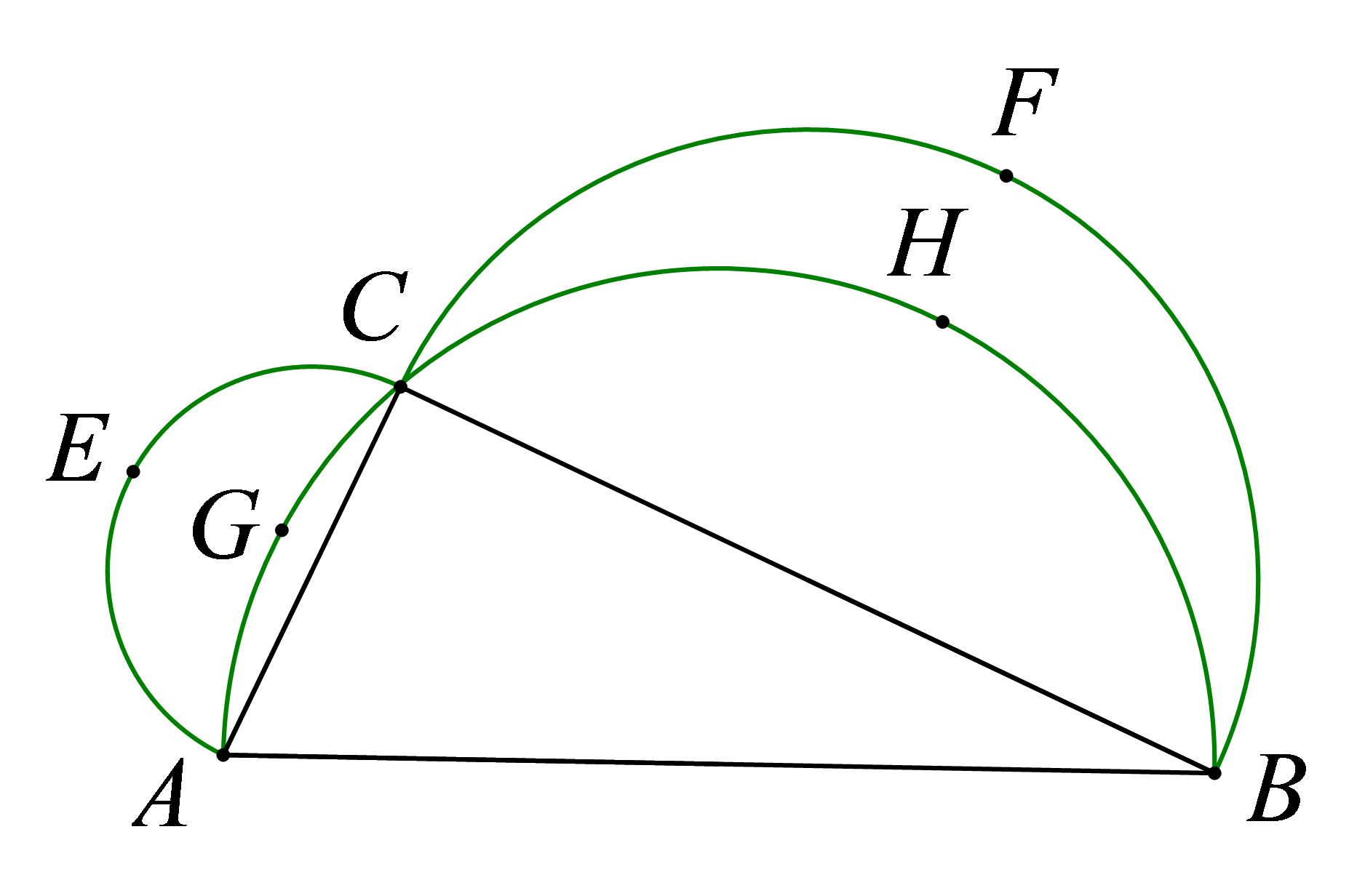
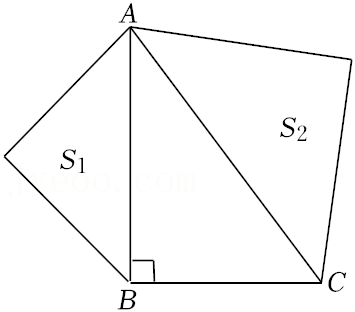
参考答案:月牙图案的面积等于两个小半圆的面积加上\(\text{Rt}△ABC\)的面积再减去大半圆的面积,再利用勾股定理,化简后即可得到:两个月牙形图案\(AGCE\)和\(BHCF\)的面积之和等于\(\text{Rt}△ABC\)的面积。
参考答案:51
参考答案:\({a^2} + {b^2} < {c^2}\)
参考答案:\(4\sqrt 3 \)
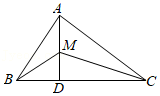
参考答案:倍长\(ED\)至\(M\),连接\(CM\),证明\(△BDE≌△CDM\),得到\(BE=CM,∠B=∠CMD\),进而\(∠MCF=90°\);
又因为\(EF=FM\),因此\(\text{Rt}△MCF\)中利用勾股定理得 \(C{M^2} + C{F^2} = F{M^2}\),故\(B{E^2} + C{F^2} = E{F^2}\)
第590题
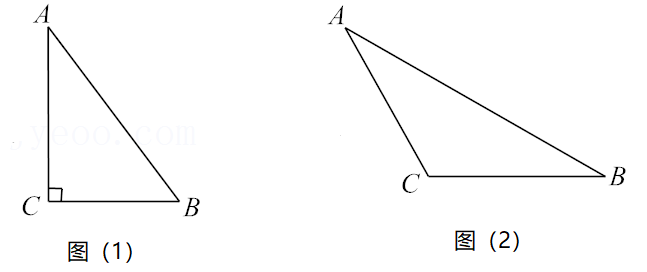
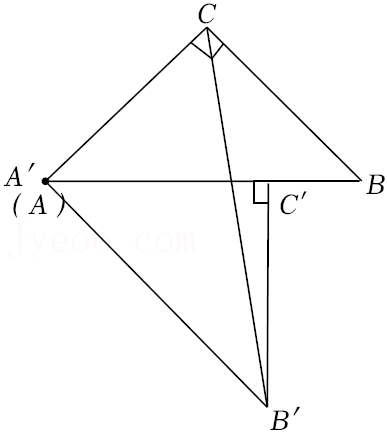
已知\(△ABC\)中, \(∠ACB=90°\),\(AC=BC=\sqrt {2}\),\(△ABD\)是等边三角形。求\(CD\)的长度。
参考答案:\(\sqrt 3 {\rm{ + }}1\)
第591题
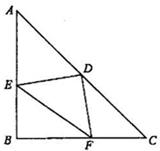
已知,如图在\(△ABC\)中,\(AB=AC\),\(∠BAC=90°\),\(∠DAE=45°\)。 求证:\(D{E^2} = B{D^2} + C{E^2}\)。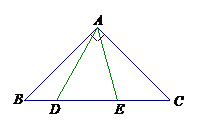
参考答案:将线段\(AD\)绕\(A\)点逆时针旋转90°,得线段\(AF\),连接\(FC、FE\)。证明\(△ABD\)全等于\(△ACF\),以及\(△ADE\)全等于\(△AFE\),即可得到。
第592题
如图,在四边形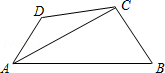
参考答案:15
参考答案:12或\(\frac{{169}}{{12}}\)
A.\(\sqrt 5 \)
B.\(\sqrt 7 \)
C.\(5\)
D.\(2\sqrt 7 \)
参考答案:D
第595题
如图,\(\angle ADB = 90^\circ \),正方形\(ABCD\)和正方形\(EFGD\)的面积分别是25和9,则以\(AG\)为直径的半圆的面积是( )。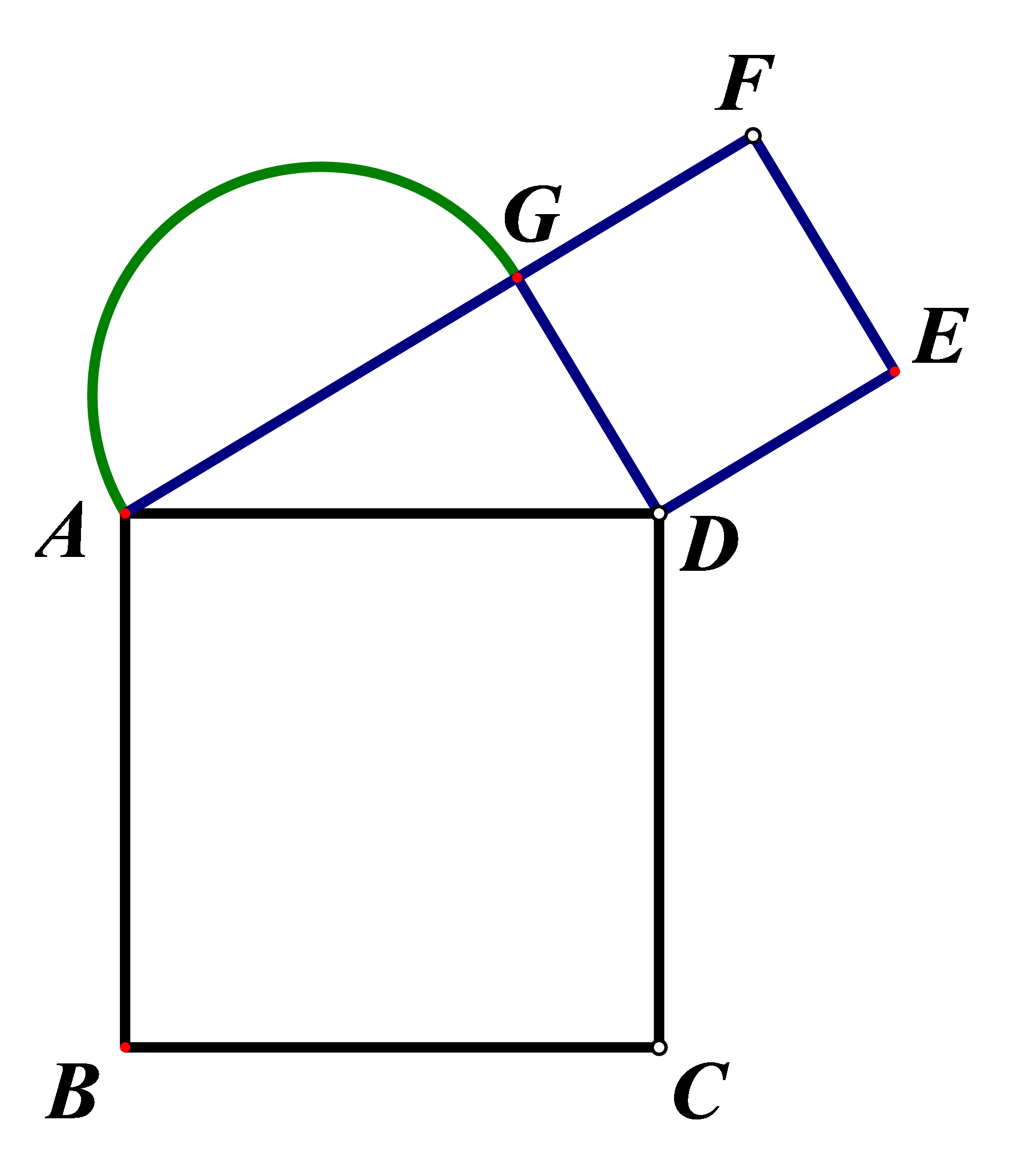
A.\(2\pi \)
B.\(4\pi \)
C.\(8\pi \)
D.\(16\pi \)
参考答案:A
第596题
如图,以\({\rm{Rt}}\Delta ABC\)的三边为直径分别向外作半圆,若斜边\(AB = 4\),则图中阴影部分的面积为\((\) \()\)。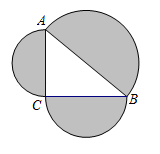
A.\(2\pi \)
B.\(4\pi \)
C.\(6\pi \)
D.\(8\pi \)
参考答案:B
参考答案:13、24或\(\frac{{169}}{{24}}\)
第600题
求证:
参考答案:证明:
\(\because AE \bot BC\),\(AF \bot CD\),
\(\therefore \angle AEB = \angle AFD\)=90°,
\(\because \)四边形\(ABCD\)是菱形,
\(\therefore AB = AD\),\(\angle B = \angle D\),
在\(\Delta ABE\)和\(\Delta ADF\)中,
\(\left\{ {\begin{array}{*{20}{l}} {\angle AEB = \angle AFD} \\ {\angle B = \angle D} \\ {AB = AD} \end{array}} \right.\),
\(\therefore \Delta ABE \cong \Delta ADF(AAS)\),
\(\therefore BE = DF\)。