初中数学八年级下册（648题）

---

已知：如图，\(D\)为\(△ABC\)的\(BC\)边中点，\(∠A=90°\)，点\(E、F\)分别在\(AB、AC\)边上，且\(DE⊥DF\)，连接\(EF\)。求证：\(E{F^2}{\rm{ = }}B{E^2} + C{F^2}\)。

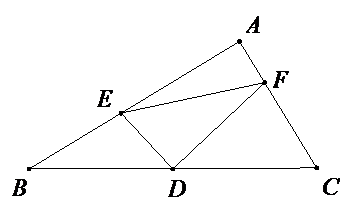
知识点：复习

参考答案：倍长\(ED\)至\(M\)，连接\(CM\)，证明\(△BDE≌△CDM\)，得到\(BE=CM，∠B=∠CMD\)，进而\(∠MCF=90°\)；

又因为\(EF=FM\)，因此\(\text{Rt}△MCF\)中利用勾股定理得 \(C{M^2} + C{F^2} = F{M^2}\)，故\(B{E^2} + C{F^2} = E{F^2}\)