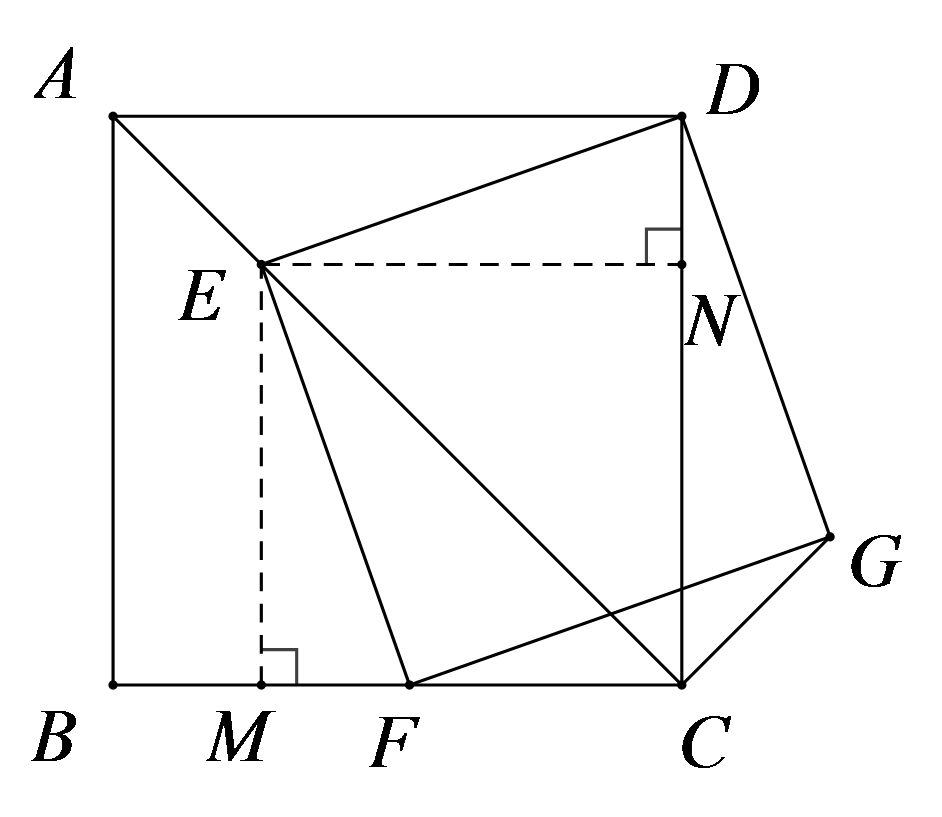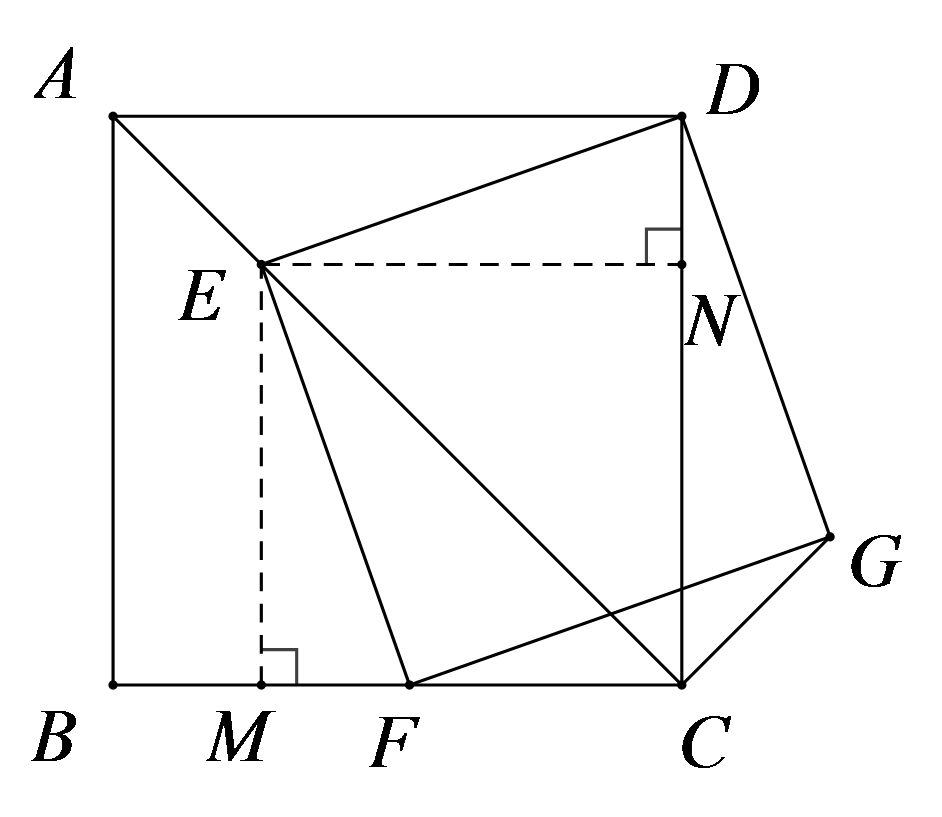证明: ∵ \(EF \bot DE\), \(DG⊥DE,FG⊥EF\),
\(∴∠DEF=∠EDG=∠EFG=90°\)
∴四边形\(DEFG\)是矩形
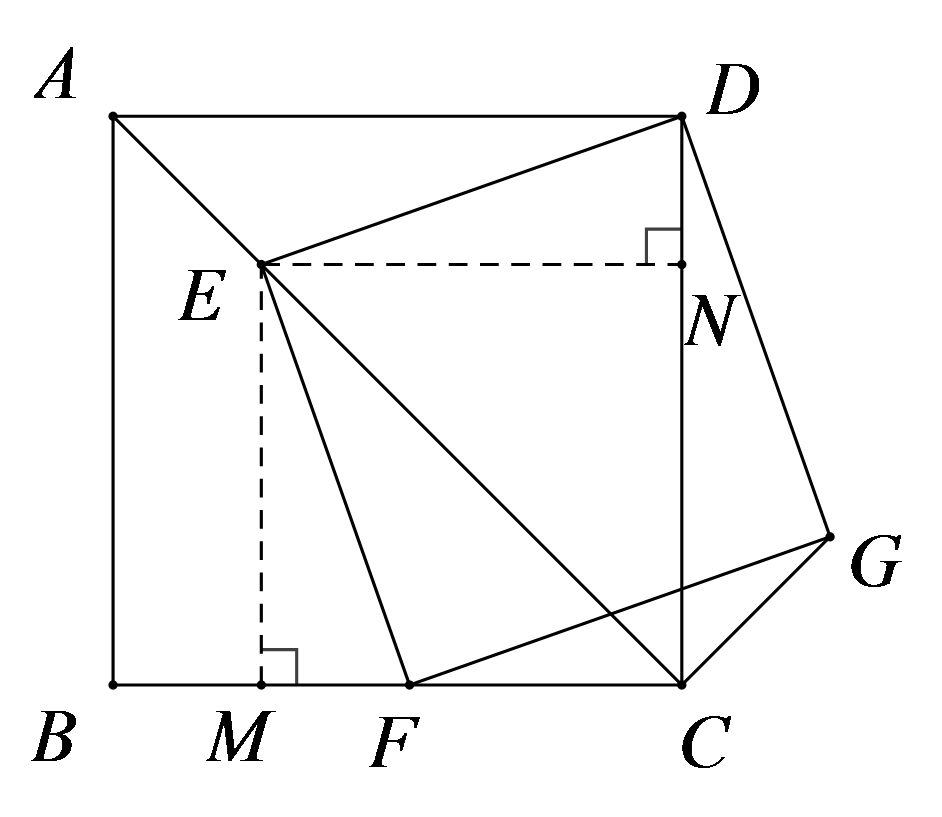
如图,作\(EM \bot BC\)于\(M\),\(EN \bot CD\)于\(N\),
\(\therefore \angle MEN = 90^\circ \),
\(\because \)点\(E\)是正方形\(ABCD\)对角线上的点,
\(\therefore EM = EN\),
\(\because \angle DEF = 90^\circ \),
\(\therefore \angle DEN = \angle MEF = 90^\circ - \angle FEN\),
\(\because \angle DNE = \angle FME = 90^\circ \),
在\(\Delta DEN\)和\(\Delta FEM\)中,
\(\left\{ {\begin{array}{*{20}{l}} {\angle DNE = \angle FME} \\ {EN = EM} \\ {\angle DEN = \angle FEM} \end{array}} \right.\),
\(\therefore \Delta DEN \cong \Delta FEM(ASA)\),
\(\therefore EF = DE\),
\(\because \)四边形\(DEFG\)是矩形,
\(\therefore \)矩形\(DEFG\)是正方形。