第261题

已知\(A = {a^2} + 4a - 8\)，\(B = - \frac{1}{2}{a^2} - 3a + 4\)，当\(a = - \frac{3}{2}\)时，求\(A - 2(A - B) + 3\)的值。

参考答案：\(\because A = {a^2} + 4a - 8\)，
\(B = - \frac{1}{2}{a^2} - 3a + 4\)，
\(\therefore \)原式\( = A - 2A + 2B + 3 = - A + 2B + 3 = - {a^2} - 4a + 8 - {a^2} - 6a + 8 + 3 = - 2{a^2} - 10a + 19\)，
当\(a = - \frac{3}{2}\)时，
原式\( = - \frac{9}{2} + 15 + 19 = 29\frac{1}{2}\)

第262题

已知多项式\((m{x^2} + nxy - 3x + y - 1) - (3{x^2} - mxy - 3x - 1)\)的差与\(x\)的取值无关，求\({( - 1)^{2008 + m + n}}[m - n + {( - n)^m}]\)的值。

参考答案：原式\( = (m - 3){x^2} + (m + n)xy + y\)，
结果与\(x\)的取值无关，
得到\(m - 3 = 0\)，
且\(m + n = 0\)，
解得：\(m = 3\)，\(n = - 3\)，则原式\( = 33\)

第263题

形如\(\left| {\begin{array}{*{20}{l}}
a&c \\
b&d
\end{array}} \right|\)的式子叫做二阶行列式，它的运算法则用公式表示为\(\left| {\begin{array}{*{20}{l}}
a&c \\
b&d
\end{array}} \right| = a \times d - b \times c\)，依此法则计算：\(\left| {\begin{array}{*{20}{l}}
{ - 2}&{ - 1} \\
3&{ - 5}
\end{array}} \right|\)。

参考答案：根据题中的新定义得：
原式\( = ( - 2) \times ( - 5) - ( - 1) \times 3 = 10 + 3 = 13\)

第264题

【简单应用】

已知\({a^2} - 2a = 1\)，则\(2{a^2} - 4a + 1 = \)___。

参考答案：3

解析：

当\({a^2} - 2a = 1\)时，\(2{a^2} - 4a + 1\)\( = 2({a^2} - 2a) + 1\)\( = 3\)

第265题

已知\(m + n = 2\)，\(mn = - 4\)，求\(2(mn - 3m) - 3(2n - mn)\)的值。

参考答案：当\(m + n = 2\)，\(mn = - 4\)时，\(2(mn - 3m) - 3(2n - mn)\)\( = 2mn - 6m - 6n + 3mn\)\( = 5mn - 6(m + n)\)\( = - 32\)

解析：

当\({a^2} - 2a = 1\)时，\(2{a^2} - 4a + 1\)\( = 2({a^2} - 2a) + 1\)\( = 3\)

第266题

【拓展提高】

参考答案：\(\because {a^2} + 2ab = - 5\)①，\(ab - 2{b^2} = - 3\)②，①\( \times 3 - \)②\( \times 2\)得\(3{a^2} + 6ab - (2ab - 4{b^2})\)\( = 3{a^2} + 4ab + 4{b^2}\)\( = - 5 \times 3 - ( - 3) \times 2\)\( = - 9\)

解析：

当\({a^2} - 2a = 1\)时，\(2{a^2} - 4a + 1\)\( = 2({a^2} - 2a) + 1\)\( = 3\)

第267题

把\({(a - b)^2}\)看成一个整体，合并\(3{(a - b)^2} - 6{(a - b)^2} + 2{(a - b)^2}\)。

参考答案：\(\because 3{(a - b)^2} - 6{(a - b)^2} + 2{(a - b)^2} = (3 - 6 + 2){(a - b)^2} = - {(a - b)^2}\)；故答案为：\( - {(a - b)^2}\)

第268题

已知\({x^2} - 2y = 4\)，求\(3{x^2} - 6y - 21\)的值。

参考答案：\(\because {x^2} - 2y = 4\)，\(\therefore \)原式\( = 3({x^2} - 2y) - 21 = 12 - 21 = - 9\)

第269题

已知\(a - 2b = 3\)，\(2b - c = - 5\)，\(c - d = 10\)，求\((a - c) + (2b - d) - (2b - c)\)的值。

参考答案：\(\because a - 2b = 3\)①，\(2b - c = - 5\)②，\(c - d = 10\)③，由①\( + \)②可得\(a - c = - 2\)，由②\( + \)③可得\(2b - d = 5\)，\(\therefore \)原式\( = - 2 + 5 - ( - 5) = 8\)

第270题

这组单项式的系数的符号规律是___，系数的绝对值规律是___；

参考答案：\({( - 1)^n}\)（或：负号正号依次出现\()\)；\(2n - 1\)（或：从1开始的连续奇数）

第271题

这组单项式的次数的规律是___；

参考答案：易得，这组单项式的次数的规律是从1开始的连续自然数

第272题

根据上面的归纳，可以猜想第\(n\)个单项式是（只能填写一个代数式）___；

参考答案：\({( - 1)^n}(2n - 1){x^n}\)

第273题

请你根据猜想，写出第2008个、第2009个单项式，它们分别是___，___。

参考答案：\(4015{x^{2008}}\)；
\( - 4017{x^{2009}}\)

第274题

在我们日常用的日历中，有许多有趣的数学规律。如在图1所示某月的日历中，用带阴影的方框圈出4个数，这四个数具有这样的性质：上下相邻的两个数相差7，左右相邻的两个数相差1，\( \ldots \)如果我们在某年某月的日历上按图2所示方式圈出4个数，若这4个数的和为78，则这4个数中最小的数为___。

参考答案：16

第275题

如果小明想的数是\( - 2\)，那么他告诉魔术师的结果应该是___；

参考答案：3

解析：

\(( - 2 \times 3 - 3) \div 3 + 6\)\( = - 3 + 6\)\( = 3\)

设这个数为\(x\)，\((3x - 3) \div 3 + 6 = 90\)解得：\(x = 85\)

第276题

如果小聪想了一个数并告诉魔术师结果为90，那么魔术师立刻说出小聪想的那个数是___；

参考答案：85

解析：

\(( - 2 \times 3 - 3) \div 3 + 6\)\( = - 3 + 6\)\( = 3\)

设这个数为\(x\)，\((3x - 3) \div 3 + 6 = 90\)解得：\(x = 85\)

第277题

观众又进行了几次尝试，魔术师都能立刻说出他们想的那个数，请你说出其中的奥妙。

参考答案：\((3a - 3) \div 3 + 6\)\( = a - 1 + 6\)\( = a + 5\)只要将给出的数据减去5，就是他们想的那个数。

解析：

\(( - 2 \times 3 - 3) \div 3 + 6\)\( = - 3 + 6\)\( = 3\)

设这个数为\(x\)，\((3x - 3) \div 3 + 6 = 90\)解得：\(x = 85\)

第278题

求\(a\)，\(b\)的值；

参考答案：根据题意得，\({x^2} - 8x + 3 + ax - b = {x^2} + (a - 8)x + 3 - b\)，
\(\because \)整式\(A + B\)中不含一次项和常数项，
\(\therefore a - 8 = 0\)，\(3 - b = 0\)，
\(\therefore a = 8\)，\(b = 3\)；

第279题

如图是去年2021年3月份的月历，用带阴影的十字方框覆盖其中5个数字，例如：1，7，8，9，15．现在移动十字方框使其履盖的5个数之和等于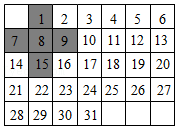\(9a + 6b\)，则此时十字方框正中心的数是___。

参考答案：18

第280题

求\(3A + 2B\)；

参考答案：\( x-5\)