第1201题 假设两个方案都可以无限重置，且是互斥项目，用等额年金法判断甲公司应采用哪个投资方案。

参考答案：见解析

解析：

因为方案一的等额年金大于方案二，所以应该选择方案一。

第1202题 计算该项目2018～2022年末的相关现金流量、净现值和现值指数（计算过程和结果填入下方表格中）。单位：万元

参考答案：见解析

解析：

第1203题 根据净现值和现值指数，判断该项目是否可行，并简要说明理由。

参考答案：见解析

解析：

净现值大于0，现值指数大于1，该项目可行。

第1204题 简要回答净现值和现值指数之间的相同点和不同点。

参考答案：见解析

解析：

相同点：①都考虑了货币时间价值和风险；②对于单一方案，决策结果相同，净现值大于0，现值指数大于1，项目可行；③净现值和现值指数在比较期限不同的项目时均有一定的局限性。

不同点：①净现值是绝对数，反映投资的效益，现值指数是相对数，反映投资的效率；②净现值法在比较投资额不同的项目时有一定的局限性，现值指数消除了投资额的差异。

第1205题 计算产品P—Ⅱ投资决策分析时适用的折现率。

参考答案：见解析

解析：

权益资本成本＝4％＋1.4×（9％－4％）＝11％

加权平均资本成本＝4/10×8％×（1－25％）＋6/10×11％＝9％

因为假设资本结构保持不变，所以产品P—Ⅱ投资决策分析时适用的折现率为加权平均资本成本9％。

第1206题 计算产品P—Ⅱ投资的初始现金流量、第5年末现金流量净额。

参考答案：见解析

解析：

初始现金流量＝－（10 000 000＋3 000 000）＝－13 000 000（元）

第5年末税法预计净残值＝10 000000×5％＝500 000（元）

因此，设备变现取得的相关现金流量＝1 000 000－（1 000 000－500 000）×25％＝875 000（元）

每年折旧＝10 000 000×（1－5％）/5＝1 900 000（元）

因此，第5年末现金流量净额＝收入×（1－所得税税率）–付现营业费用×（1－所得税税率）＋折旧×所得税税率＋营运资本回收＋设备变现取得的相关现金流量－“P一Ⅰ”每年营业现金毛流量的减少＝50000×300×（1－25％）－（600 000＋200×50 000）×（1－25％）＋1 900 000×25％＋3 000 000＋875 000－545000＝7 105 000（元）

第1207题 计算产品P—Ⅱ投资的净现值。

参考答案：见解析

解析：

产品P一Ⅱ第1～4年的现金流量净额＝50000×300×（1－25％）－（600 000＋200×50 000）×（1－25％）＋1 900 000×25％－545 000＝3 230 000（元）

净现值＝3 230 000×（P/A，9％，4）＋7 105 000×（P/F，9％，5）－13 000 000＝2 081 770.5（元）。

第1208题 计算无风险利率。

参考答案：见解析

解析：

无风险利率应当选择上市交易的10年期长期政府债券的到期收益率作为代替。

设10年期长期政府债券的到期收益率为i，则有：

NPV＝1 000×6％×（P/A，i，10）＋1 000×（P/F，i，10）－1 120

当i＝4％时，NPV＝60×8.1109＋1000×0.6756－1 120＝42.25（元）

当i＝5％时，NPV＝60×7.7217＋1000×0.6139－1 120＝－42.80（元）

根据内插法：（i－4％）/（5％－4％）＝（0－42.25）/（－42.80－42.25）

求得：到期收益率i＝4.5％

第1209题 使用可比公司法计算锂电池行业代表企业的平均β资产、该锂电池项目的β权益与权益资本成本。

参考答案：见解析

解析：

乙公司卸载财务杠杆的β_资产＝1.5/[1＋40/60×（1－25％）]＝1

丙公司卸载财务杠杆的β_资产＝1.54/[1＋50/50×（1－25％）]＝0.88

锂电池行业代表企业的平均β_资产＝（1＋0.88）/2＝0.94

该锂电池项目的β_权益＝0.94×[1＋30/70×（1－25％）]＝1.24

该锂电池项目的权益资本成本＝4.5％＋1.24×7％＝13.18％

第1210题 计算该锂电池项目的加权平均资本成本。

参考答案：见解析

解析：

该锂电池项目的加权平均资本成本＝9％×（1－25％）×30％＋13.18％×70％＝11.25％。

第1211题 为该公司是否更新设备做出决策。

参考答案：见解析

解析：

（1）△年折旧＝（220 000－40 000）/6-（96 000－6 000）/10＝21 000（元）

（2）△初始投资＝220 000－30 000－（60000－30 000）×25％＝182 500（元）

（3）新设备使用期满的残值收入带来的流入＝35 000＋（40 000－35000）×25％＝36 250（元）

旧设备使用期满的残值收入带来的流入＝0＋（6 000－0）×25％＝1 500（元）

△残值流入＝36 250－1 500＝34 750（元）

各年营业现金毛流量的增量

单位：元

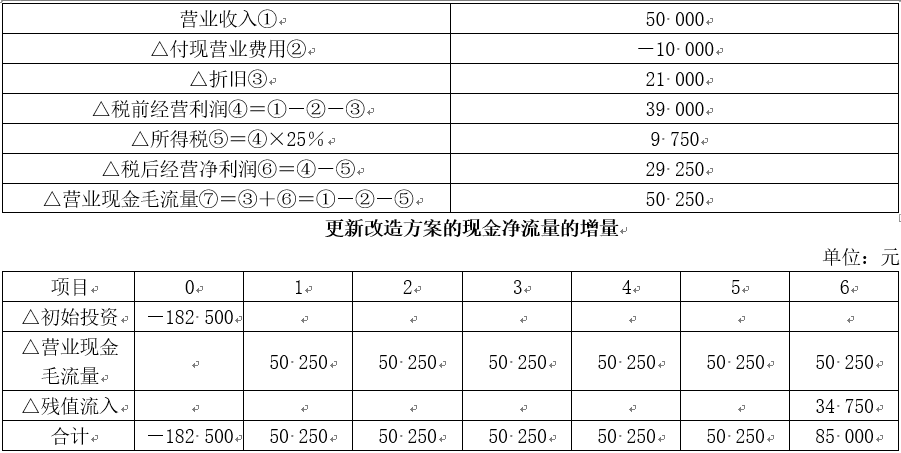
（4）

方法一：根据净现值法进行决策。

△净现值＝―182 500＋50250×（P/A，12％，5）＋85 000×（P/F，12％，6）＝－182 500＋50 250×3.6048＋85 000×0.5066＝41 702.2（元）

可见，更新改造方案的净现值大于零，因此应该更新改造。

方法二：根据内含报酬率法进行决策。

△净现值＝一182 500＋50250×（P/A，i，5）＋85 000×（P/F，i，6）

当i＝20％，△净现值＝―182 500＋50250×（P/A，20％，5）＋85 000×（P/F，20％，6）＝－182 500＋50 250×2.9906＋85 000×0.3349＝－3 755.85（元）

当i＝18％，△净现值＝―182 500＋50250×（P/A，18％，5）＋85 000×（P/F，18％，6）＝－182 500＋50 250×3.1272＋85 000×0.3704＝6 125.8（元）

更新改造方案的内含报酬率＝18％＋（0－6 125.8）/（－3 755.85－6 125.8）×（20％－18％）＝19.24％

可见，更新改造方案的内含报酬率19.24％大于该公司要求的最低投资报酬率12％，因此应该更新改造。

第1212题 分别计算采用甲、乙设备的平均年成本，并据此判断应当购买哪一种设备。

参考答案：见解析

解析：

第1213题 计算评价汽车制造厂建设项目的必要报酬率（计算时β值取小数点后4位）。

参考答案：见解析

解析：

由于该公司投资项目评价采用实体现金流量法，因此，折现率应采用加权平均资本成本。计算该项目的必要报酬率，也就是计算该项目的加权平均资本成本。

解法1：

首先计算W公司分别以A、B、C公司为参照物得出的3个β_权益；然后将上述3个β_权益的平均值作为本项目的β_权益，代入资本资产定价模型计算得出本项目的权益资本成本；最后计算得出本项目的加权平均资本成本（即项目的必要报酬率）。

A公司β_资产＝1.1000/[1＋（1－15％）×4/6]＝0.7021

W公司的β_权益＝0.7021×[1＋（1－25％）×4/6]＝1.0532

B公司β_资产；p＝1.2000/[1＋（1－25％）×5/5]＝0.6857

W公司的β_权益＝0.6857×[1＋（1－25％）×4/6]＝1.0286

C公司β_资产＝1.4000/[1＋（1－20％）×6/4]＝0.6364

W公司的β_权益＝0.6364×[1＋（1－25％）×4/6]＝0.9546

本项目的β_权益＝（1.0532＋1.0286＋0.9546）/3＝1.0121

权益资本成本＝5％＋1.0121×10％＝15.12％

加权平均资本成本＝10％×（1－25％）×40％＋15.12％×60％＝12.07％。

解法2：

首先计算W公司分别以A、B、C公司为参照物得出的3个β_权益；其次将上述3个β_权益分别代入资本资产定价模型，计算得出本项目的3个权益资本成本；然后计算得出本项目的3个加权平均资本成本，最后取其算术平均数即本项目的必要报酬率。

A公司β_资产＝1.1000/[1＋（1－15％）×4/6]＝0.7021

W公司的β_权益＝0.7021×[1＋（1－25％）×4/6]＝1.0532

权益资本成本＝5％＋1.0532×10％＝15.53％

加权平均资本成本＝10％×（1－25％）×40％＋15.53％×60％＝12.32％

B公司β_资产＝1.2000/[1＋（1－25％）×5/5]＝0.6857

W公司的β_权益＝0.6857×[1＋（1－25％）×4/6]＝1.0286

权益资本成本＝5％＋1.0286×10％＝15.29％

加权平均资本成本＝10％×（1－25％）×40％＋15.29％×60％＝12.17％

C公司β_资产＝1.4000/[1＋（1－20％）×6/4]＝0.6364

W公司的β_权益＝0.6364×[1＋（1－25％）×4/6]＝0.9546

权益资本成本＝5％＋0.9546×10％＝14.55％

加权平均资本成本＝10％×（1－25％）×40％＋14.55％×60％＝11.73％

本项目的必要报酬率＝（12.32％＋12.17％＋11.73％）/3＝12.07％。

第1214题 在考虑货币时间价值的情况下，分别计算设备更新年限为1年、2年、3年的平均年成本。

参考答案：见解析

解析：

年折旧＝300×（1－5％）/3＝95（万元），

年折旧抵税额＝95×25％＝23.75（万元），

第1年末残值变现损失抵税额＝（300－95－200）×25％＝1.25（万元），

第2年末残值变现损失抵税额＝（300－95×2－110）×25％＝0（万元），

第3年末残值变现收益纳税额＝（40－300×5％）×25％＝6.25（万元），

更新年限为1年的平均年成本

＝[300－（200＋1.25）×（P/F，10％，1）＋90×（1－25％）×（P/F，10％，1）－23.75×（P/F，10％，1）]/（P/A，10％，1）

＝[300－（200＋1.25）×0.9091＋90×（1－25％）×0.9091－23.75×0.9091]/0.9091

＝172.5（万元），

更新年限为2年的平均年成本

＝[300－110×（P/F，10％，2）＋90×（1－25％）×（P/F，10％，1）＋100×（1－25％）×（P/F，10％，2）－23.75×（P/A，10％，2）]/（P/A，10％，2）

＝（300－110×0.8264＋67.5×0.9091＋75×0.8264－23.75×1.7355）/1.7355

＝167.8（万元），

更新年限为3年的平均年成本

＝[300－（40－6.25）×（P/F，10％，3）＋90×（1－25％）×（P/F，10％，1）＋100×（1－25％）×（P/F，10％，2）＋150×（1－25％）×（P/F，10％，3）－23.75×（P/A，10％，3）]/（P/A，10％，3）

＝（300－33.75×0.7513＋67.5×0.9091＋75×0.8264＋112.5×0.7513－23.75×2.4869）/2.4869

＝170.27（万元）。

第1215题 根据要求（1）计算的平均年成本，确定该设备的经济寿命。

参考答案：见解析

解析：

更新年限为2年的平均年成本最低，因此该设备的经济寿命为2年。

第1216题 计算新、旧机床现金流出的总现值。

参考答案：见解析

解析：

计算保留旧机床方案的现金流出总现值（单位：元）。

第1217题 进行方案的选择。

参考答案：见解析

解析：

在两方案营业收入一致的情况下，新设备现金流出总现值为74 962.22元，旧设备现金流出总现值为70567.21元。因此，继续使用旧设备比较经济。

第1218题 计算债务税后资本成本、股权资本成本和项目加权平均资本成本。

参考答案：见解析

解析：

第1219题 计算项目2016年及以后各年末现金净流量及项目的净现值，并判断该项目是否可行（计算过程和结果填入下方表格）。 
各年末现金净流量及项目净现值 单位：万元

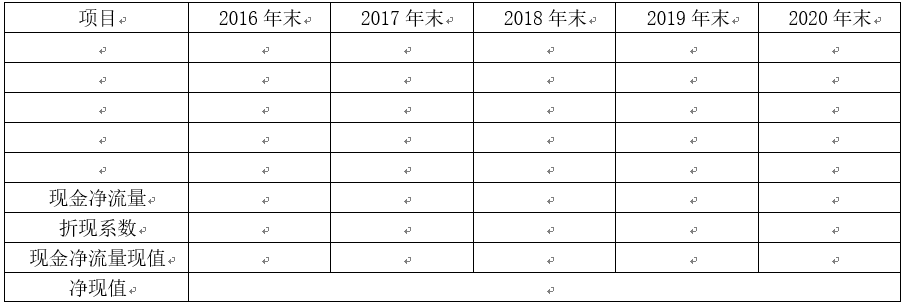
参考答案：见解析

解析：

年折旧额＝4 000×（1－5％）/4＝950（万元）

项目终结点的账面价值＝4 000－950×3＝1 150（万元）       

     各年末现金净流量及项目净现                                          单位：万元

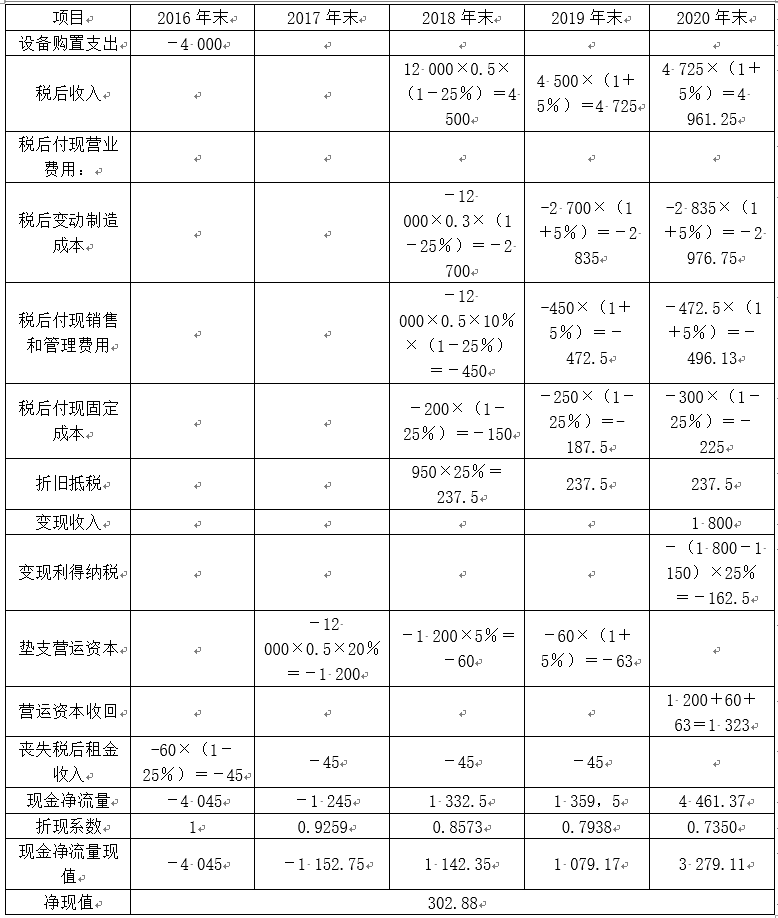
因为该项目净现值大于零，所以该项目可行。

第1220题 假设其他条件不变，利用最大最小法计算生产线可接受的最高购置价格。

参考答案：见解析

解析：

设增加的购置成本为X万元

年折旧＝（4 000＋X）×（1－5％）/4＝950＋X×（1－5％）/4＝950＋0.2375X

年折旧抵税＝（950＋0.2375X）×25％＝237.5＋0.059375X

增加的折旧抵税＝0.059375X

终结点账面价值＝（4 000＋X）－（950＋0.2375X）×3＝1 150＋0.2875X

变现价值＝1 800万元

变现相关现金流量＝1 800－（1800－1 150－0.2875X）×25％＝1 637.5＋0.071875X

增加的变现相关现金流量＝0.071875X

则：－302.88＝－X＋0.059375X×（P/A，8％，3）×（P/F，8％，1）＋0.071875X×（P/F，8％，4）

即：－302.88＝一X＋0.059375X×2.5771×0.9259＋0.071875X×0.7350

求得：X＝376.02（万元），该生产线可接受的最高购置价格为4 376.02万元（4 000＋376.02）。