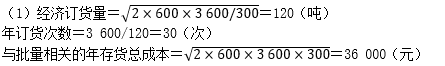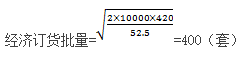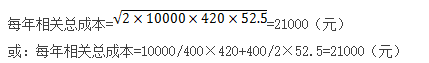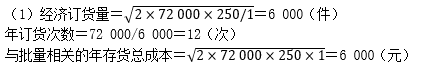“微信扫一扫”进入考试题库练习及模拟考试
注册会计师《财务成本管理》题库(1478题)
参考答案:见解析
解析:
(1)X的经济订货量==120(吨)
年订货次数=3 600/120=30(次)
与批量相关的年存货总成本==36 000(元)
(2)每天需求量=3 600/360=10(吨)
保险储备为0时,平均缺货量=10×10%+20×10%=3(吨)
相关总成本=3×1 000×30-90 000(元)
保险储备为10吨时,平均缺货量=10%×10%=1(吨)
相关总成本=1×1 000×30+10×300=33 000(元)
保险储备为20吨时,不会发生缺货,此时相关总成本=20×300=6 000(元)
可见,保险储备为20吨时相关总成本最小,所以,最佳保险储备量20吨。
第942题
A企业每年耗用某种原材料1 000千克,该材料的单位成本为15元,单位变动储存成本为2元,一次订货成本90元,则下列说法正确的是( )。
A.该企业的经济订货批量为300千克,与批量有关的存货总成本为600元
B.该企业的经济订货批量为300千克,与批量有关的存货总成本为4 500元
C.该企业的经济订货批量为600千克,与批量有关的存货总成本为300元
D.该企业的经济订货批量为600千克,与批量有关的存货总成本为9 000元
参考答案:A
解析:
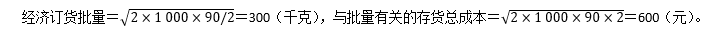
第944题
(2)计算X材料不同保险储备量的年相关总成本,并确定最佳保险储备量。
参考答案:见解析
解析:
(2)每天平均需求量=3600/360=10(吨)
当保险储备B=0时,TC(S、B)=30×(10%×10+10%×10×2)×1 000=90 000(元)
当保险储备B=10吨时,TC(S、B)=30×(10%×10)×1 000+10×300=33 000(元)
当保险储备B=20吨时,TC(S、B)=20×300=6 000(元)
因为当保险储备量为20吨时,保险储备的年相关总成本最低,所以最佳保险储备量为20吨。
第945题
下列各项因素中,与订货提前期有关的是( )。
A.经济订货量
B.再订货点
C.订货次数
D.订货间隔期
参考答案:B
解析:
订货提前期对每次订货量、订货次数、订货时间间隔不产生影响,由此可知选项ACD不是答案;在提前订货的情况下,企业再次发出订货单时,尚有存货的库存量,称为再订货点,由此可知,选项B是答案。
第951题
计算每年与储备存货相关的总成本。
参考答案:见解析
解析:
每年与储备存货相关的总成本=总购置成本+总订货成本+总储存成本
=10000×395+(10000/400×420+10760+3000×12)+[52.5×(400/2+100)+2500]
=3950000+57260+18250=4025510(元)
第954题
研究保险储备的目的,就是要找出合理的保险储备量,使缺货或供应中断损失和储备成本之和最小。需要考虑( )。
A.单位缺货成本
B.单位储存变动成本
C.交货期
D.存货年需求量
参考答案:ABCD
解析:
保险储备量储备成本=保险储备量×单位储存变动成本(由此可知,选项B是答案),缺货或供应中断损失=单位缺货成本×一次订货缺货量×年订货次数(由此可知,选项A是答案),年订货次数=存货年需要量/经济订货量(由此可知,选项D是答案),计算“一次订货缺货量”时需要知道交货期内的平均需要量(由此可知,选项C是答案)。
参考答案:见解析
解析:
(1)经济订货量=[(2×720×500)/200]=60(吨)
最佳订货次数=720÷60=12(次)
平均日需求量=720÷360=2(吨)
交货期长度及其需求量的概率分布如下:

保险储备量=0,再订货点=2×10=20(吨)
一次订货缺货量=2×30%+4×20%=1.4(吨)
缺货成本=1.4×50×12=840(元)
保险储备成本=0
缺货成本+保险储备成本=840(元)
保险储备量=2(吨),再订货点=2×10+2=22(吨)
一次订货缺货量=2×20%=0.4(吨)
缺货成本=0.4×50×12=240(元)
保险储备成本=2×200=400(元)
缺货成本+保险储备成本=240+400=640(元)
保险储备量=4(吨),再订货点=2×10+4=24(吨)
一次订货缺货量=0
缺货成本=0
保险储备成本=4×200=800(元)
缺货成本+保险储备成本=800(元)
经比较,设置2吨保险储备时的缺货成本与保险储备成本之和最低,应设置2吨的保险储备。
购置成本=720×(3000+100)=2232000(元)
与批量有关的存货总成本=60×200=12000(元)
缺货成本+保险储备成本=240+400=640(元)
总成本=2232000+12000+640=2244640(元)
(2)经济订货量= 【(2×720×100)/200×(1-2/10)】=30(吨)
与批量有关的存货总成本=30×200×(1-2/10)=4800(元)
购置成本=720×(3300+20)=2390400(元)
总成本=2390400+4800=2395200(元)
(3)方案一的总成本低于方案二的总成本,应当选择方案一。
第957题
存货订货量决策中,下列关于保险储备的表述正确的有( )。
A.保险储备增加,存货的缺货损失减小
B.保险储备增加,存货中断的概率变小
C.保险储备增加,存货的再订货点降低
D.保险储备增加,存货的储存成本提高
参考答案:ABD
解析:
较高的保险储备可降低存货中断的概率和存货中断的损失,即降低缺货损失,但也增加了存货的储存成本。因此,选项A、B、D正确。再订货点=预计交货期内的需求+保险储备,因此保险储备增加,存货的再订货点提高,选项C错误。
第958题
要求:假设考虑缺货的影响,丙公司自制与外购方案哪个成本低?
参考答案:见解析
解析:
(1)平均每天需要量=14400/360=40(件),
自制相关总成本=14 400×10+[2×14 400×34.375×4×(1-40/128)]1/2=145 650(元)。
(2)外购的经济订货批量=(2×14 400×72/4)1/2=720(件),
每年订货次数=14 400/720=20(次),
交货期内的平均每天需要量=14 400/360=40(件)。
如果延迟交货1天,则交货期为10+1=11(天),交货期内的需要量=11×40=440(件),概率为0.25;
如果延迟交货2天,则交货期为10+2=12(天),交货期内的需要量=12×40=480(件),概率为0.1;
如果延迟交货3天,则交货期为10+3=13(天),交货期内的需要量=13×40=520(件),概率为0.05。
①保险储备B=0时,再订货点R=10×40=400(件);
S=(440-400)×0.25+(480-400)×0.1+(520-400)×0.05=24(件),
TC(S,B)=24×5×20+0×4=2 400(元)。
②保险储备B=40时,再订货点眼=400+40=440(件),
S=(480-440)×0.1+(520-440)×0.05=8(件),
TC(S,B)=8×5×20+40×4=960(元)。
③保险储备B=80时,再订货点R=400+80=480(件),
S=(520-480)×0.05=2(件),
TC(S,B)=2×5×20+80×4=520(元)。
④保险储备B=120时,再订货点R=400+120=520(件),
S=0,
TC(S,B)=120×4=480(元)。
通过比较得出,最合理的保险储备为120件,再订货点为520件。
考虑缺货情况下,外购相关总成本=14 400×9.82+(2×14 400×72×4)1/2+480=144 768(元),
可见,外购方案的成本低。