第221题

为了解 2020 年高校毕业生的就业情况，校学生处拟从全校 5000 名毕业生中随机抽取 1%的学生进行调查。不重复抽样条件下可能的样本个数是（    ）。

A.50

B.5000

C.5000^2

D.

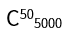
参考答案：D

解析：

5000*1%=50，在不重复抽样过程中，共有C_N^n=N!/n!(N-n)!个可能的样本，带入即为D选项。

第222题 如果总体服从正态分布，样本均值一定服从正态分布。

参考答案：对

解析：我们可以证明当总体服从正态分布时，样本均值一定服从正态分布。

第223题

当总体为未知的非正态分布，样本容量n充分大时，样本均值的标准差为总体标准差的（ ）。

A.1/n

B.

C.n/N

D.N-n/N-1

参考答案：B

解析：

若总体为未知的非正态分布，只要样本容量n足够大（通常要求 n≥30），样本均值仍会接近正态分布，其分布的期望值为总体均值，方差为总体方差的1/n。这就是统计上的中心极限定理： 从均值为μ，方差为σ²的总体中，抽样样本量为n的随机样本，当n充分大时，样本均值的分布近似服从均值为μ，方差为σ²/n的正态分布。

第224题

统计量是样本的函数。(   )

参考答案：对

解析：

统计量是根据样本数据计算的用于推断总体的某些量，是对样本特征的某个概括性度量。因此，统计量是样本的函数。

第225题

对一部贺岁片收视率进行调查，随机抽取100人，其中有20人没有看过这部贺岁片，则看过这部贺岁片人数比率的点估计值为(  )。

A.20%

B.20

C.80

D.80%

参考答案：D

解析：

点估计就是用样本统计量的实现值来近似相应的总体参数。本题中，样本为随机抽取的100人，有20人没有看过该部贺岁片，则看过这部贺岁片的人数有80人，因此看过这部贺岁片人数比率的点估计值为80/100= 80%。

第226题

区间估计不仅给出了未知参数的估计范围，而且还可以给出该范围包含参数真值的可信程度。(   )  

参考答案：对

解析：

区间估计：根据估计可靠程度的要求，利用随机抽取的样本的统计量值确定能够覆盖总体参数的可能区间的一种估计方法。是在点估计的基础上，给出总体参数估计的一个区间范围，该区间通常由样本统计量加减估计误差得到。与点估计不同，进行区间估计时，根据样本统计量的抽样分布可以对样本统计量与总体参数的接近程度给出一个概率度量。

第227题

在参数估计中，无偏性是衡量一个估计量是否理想的惟一准则。(  )

参考答案：错

解析：

评价估计量的标准有：①无偏性，是指估计量抽样分布的期望值等于被估计的总体参数；②有效性，是指估计量的方差尽可能小；③一致性，是指随着样本量的增大，点估计量的值越来越接近被估计总体的参数。

第228题

对某单位职工的文化程度进行抽样调查，得知其中80%的人是高中毕业，抽样平均误差为2%，当置信度为95.45%时(z=2)，该单位职工中具有高中文化程度的比重是 ()。

A.大于84%

B.等于78%

C.在76%～84%之间

D.在78%～82%之间

参考答案：C

解析：

该单位职工中具有高中文化程度的比重的置信区间为：

第229题

评价估计量的标准为(  )。

A.一致性

B.无偏性

C.显著性

D.有效性

E.综合性

参考答案：ABD

解析：

评价估计量的标准包括：①无偏性，是指估计量抽样分布的期望值等于被估计的总体参数；②有效性，是指估计量的方差尽可能小；③一致性，是指随着样本量的增大，点估计量的值越来越接近被估计总体的参数。

第230题

当正态总体的方差未知，且为小样本条件下，构造总体均值的置信区间使用的分布是(  )。

A.正态分布

B.t分布

C.χ2分布

D.F分布

参考答案：B

解析：

如果总体方差未知，且为小样本条件下，需要用样本方差代替总体方差，样本均值经过标准化以后的随机变量服从自由度为(n -1)的t分布，需要采用t分布来建立总体均值的置信区间。

第231题

区间估计中总体指标所在范围(   )

A.是一个可能范围

B.是绝对可靠的范围

C.不是绝对可靠的范围

D.是有一定把握程度的范围

E.是毫无把握的范围

参考答案：ACD

解析：

区间估计就是根据估计可靠程度的要求，利用随机抽取的样本的统计量值确定能够覆盖总体参数的可能区间的一种估计方法。它是包括样本统计量在内（有时是以统计量为中心）的一个区间，该区间通常是由样本统计量加减估计标准误差得到的。

第232题

有效性是指估计量的方差尽可能小。（  ）

参考答案：对

解析：

有效性是指估计量的方差尽可能小。一个无偏的估计量并不意味着它就非常接近被估计的总体参数，估计量与参数的接近程度使用估计量的方差来度量的。对同一个总体参数的两个无偏估计量，有更小方差的估计量更有效。

第233题 为了解某市市民的通勤时间（单位：分钟），某咨询公司随机抽取了5000名市民进行调查，以95%的置信水平推断市民上班平均乘车时间的置信区间为（58，115）。则下列说法正确的是（ ）。

A.有95%的把握认为样本均值在58分钟至115分钟之间

B.对于这个样本，95%的市民上班所需的乘车时间在58分钟至115分钟之间

C.如果重复选取容量为5000的随机样本，则95%的样本均值会在58分钟至115分钟之间

D.如果重复选取容量为5000的随机样本，则95%的置信区间会包含总体均值的真值

参考答案：D

解析：根据正态分布3δ准则，被调查者上班时间在2个标准差(28)的范围是95.45%，即被调查者中有95.45%的人的上班时间是在离总体均值左右2个标准差的范围里。样本量给定时，置信区间的宽度随着置信水平的增大而增大;当置信水平固定时，置信区间的宽度随样本量的增大而减小。但是，并不是所有的区间都包含总体参数的真值，因为总体参数的真值是固定的、未知的，而用样本构造的区间则是随机的，置信区间就是一个随机区间。当a取5%时，只能说使用某种方法构造的所有区间中有95%的区间包含总体参数的真值，5%的区间不包含总体参数的真值。

第234题 在其他条件不变的情况下，当样本量增大时，总体均值的置信区间（ ）。

A.保持不变

B.变小

C.变大

D.可能变大也可能变小

参考答案：B

解析：当样本量给定时，置信区间的宽度随着置信水平的增大而增大;当置信水平固定时，置信区间的宽度随样本量的增大而减小。

第235题

设总体X～N(u，σ²），基于来自总体X的容量为16的简单随机样本，测得样本均值= 31.645，样本方差S²=0.09，则总体均值μ的置信度为0.98的置信区间为(  )。t≈2.6

A.(30.88, 32.63)

B.(31.45, 31.84)

C.(31.62, 31.97)

D.(30.45, 31.74)

参考答案：B

解析：

第236题

标准化公式为（）。

参考答案：对

解析：

对样本均值的正态分布进行标准化：

第237题

小样本情况下，总体均值的区间估计方法是（    ）。

A.

B.

C.

D.

E.

参考答案：AD

解析：

第238题

由样本统计量来估计总体参数时，要求估计量的方差尽可能的小，则方差是用来评价估计量标准的(  )。

A.无偏性

B.一致性

C.同质性

D.有效性

参考答案：D

解析：

有效性是指估计量的方差尽可能小。一个无偏的估计量并不意味着它就非常接近被估计的总体参数，估计量与参数的接近程度使用估计量的方差来度量的。对同一个总体参数的两个无偏估计量，有更小方差的估计量更有效。

第239题 对新华中学学生的视力进行了一次抽样调查。根据调查数据估计出学生近视率 95%的置信区间为（55%，68%），则说明总体比例将落在这个置信区间。

参考答案：错

解析：说明95%的置信区间会包含总体均值的真值。

第240题

估计量的有效性与其方差无关。(  )

参考答案：错

解析：

有效性是指估计量的方差尽可能小。一个无偏的估计量并不意味着它就非常接近被估计的总体参数，估计量与参数的接近程度使用估计量的方差来度量的。对同一个总体参数的两个无偏估计量，有更小方差的估计量更有效。