第21题

参考答案：由（1）知，分成三堆的方法有 \({\rm{C}}_6^1{\rm{C}}_5^2{\rm{C}}_3^3\) 种，而每种分组方法仅对应一种分配方法，故甲得1本，乙得2本，丙得3本的分法亦为 \({\rm{C}}_6^1{\rm{C}}_5^2{\rm{C}}_3^3 = 60\) 种.

第22题

参考答案：3个人一个一个地来取书，甲从6本不同的书中任取出2本的取法有 \({\rm{C}}_6^2\) 种，乙再从余下的4本书中取2本书，有 \({\rm{C}}_4^2\) 种取法，丙从余下的2本中取2本书，有 \({\rm{C}}_2^2\) 种取法，所以一共有 \({\rm{C}}_6^2{\rm{C}}_4^2{\rm{C}}_2^2 = 90\) 种取法.

第23题

参考答案：把6本不同的书分成三堆，每堆2本与把6本不同的书分给甲、乙、丙三人，每人2本的区别在于，后者相当于把6本不同的书平均分成三堆后，再把书分给甲、乙、丙三人，因此，设把6本不同的书，平均分成三堆的方法有x种，那么把6本不同的书分给甲、乙、丙三人每人2本的分法就应有 \(x{\rm{A}}_3^3\) 种，由（4）知，把6本不同的书分给甲、乙、丙三人，每人2本的方法有 \({\rm{C}}_6^2{\rm{C}}_4^2{\rm{C}}_2^2\) 种.所以 \(x{\rm{A}}_3^3 = {\rm{C}}_6^2{\rm{C}}_4^2{\rm{C}}_2^2\) ，则 \(x = \frac{{{\rm{C}}_6^2{\rm{C}}_4^2{\rm{C}}_2^2}}{{{\rm{A}}_3^3}} = 15\) .

第24题

参考答案：297 \(2A_5^5 + 2A_4^4 + A_3^3 + A_2^2 + A_1^1 = 297\)

第25题

参考答案：9

先把1填入方格中，符合条件的有3种方法，第二步把被填入方格的对应数字填入其它三个方格，又有三种方法；第三步填余下的两个数字，只有一种填法，共有3×3×1=9种填法

把元素排到指定位置上，可先把某个元素按规定排入，第二步再排另一个元素，如此继续下去，依次即可完成。

第26题

参考答案：37种考虑走3级台阶的次数：
1）有0次走3级台阶（即全走2级），那么有1种走法；
2）有1次走三级台阶。（不可能完成任务）；
3）有两次走3级台阶，则有5次走2级台阶：
（a）两次三级台阶挨着时：相当于把这两个挨着的三级台阶放到5个两级台阶形成的空中，有 \(C_6^1 = 6\) 种
（b）两次三级不挨着时：相当于把这两个不挨着的三级台阶放到5个两级台阶形成的空中，有 \(C_6^2 = 15\) 种走法。
4）有3次（不可能）
5）有4次走3级台阶，则有2次走两级台阶，互换角色，想成把两个2级台阶放到3级台阶形成得空中，同（3）考虑挨着和不挨着两种情况有种 \(C_5^1 + C_5^2 = 15\) 走法；
6）有5次（不可能） 故总共有：1+6+15+15=37种。

第27题

A.60

B.150

C.540

D.\( {3}^{5}\)

参考答案：B

解析：

第28题

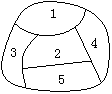
参考答案：72

解析：

第29题

A.70种

B.64种

C.58种

D.52种

参考答案：C

解析：

第30题

参考答案：199个 10演员中有5人只会唱歌，2人只会跳舞3人为全能演员。选上唱歌人员为标准进行研究，只会唱的5人中没有人选上唱歌人员共有 \(C_3^2C_3^2\) 种,只会唱的5人中只有1人选上唱歌人员 \(C_5^1C_3^1C_4^3\) 种,只会唱的5人中只有2人选上唱歌人员有 \(C_5^2C_5^2\) 种，由分类计数原理共有 \(C_3^2C_3^2 + C_5^1C_3^1C_4^3 + C_5^2C_5^2\)=199种。