“微信扫一扫”进入考试题库练习及模拟考试
高中数学 必修 第二册(415题)
第145题
在调查中发现
A.男人、女人中患色盲的频率分别为 \(0.038,0.006\)
B.男、女患色盲的概率分别为\(\frac{{19}}{{240}}\),\(\frac{3}{{260}}\)
C.男人中患色盲的比例比女人中患色盲的比例大,患色盲与性别是有关的
D.不能说明患色盲与性别是否有关
参考答案:C
A.0.005
B.0.01
C.0.025
D.0.05
参考答案:D
第147题
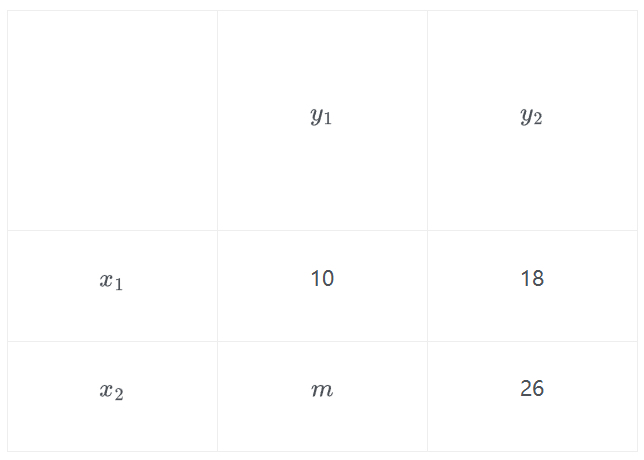
某村庄对该村内50名老年人、年轻人每年是否体检的情况进行了调查,统计数据如表所示: 已知抽取的老年人、年轻人各 \(25\) 名,则对列联表数据的分析错误的是( )
A.\(a=18\)
B.\(b=19\)
C.\(c+d=50\)
D.\(e-f=2\)
参考答案:D
第148题
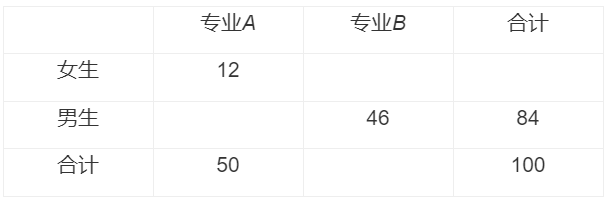
为考查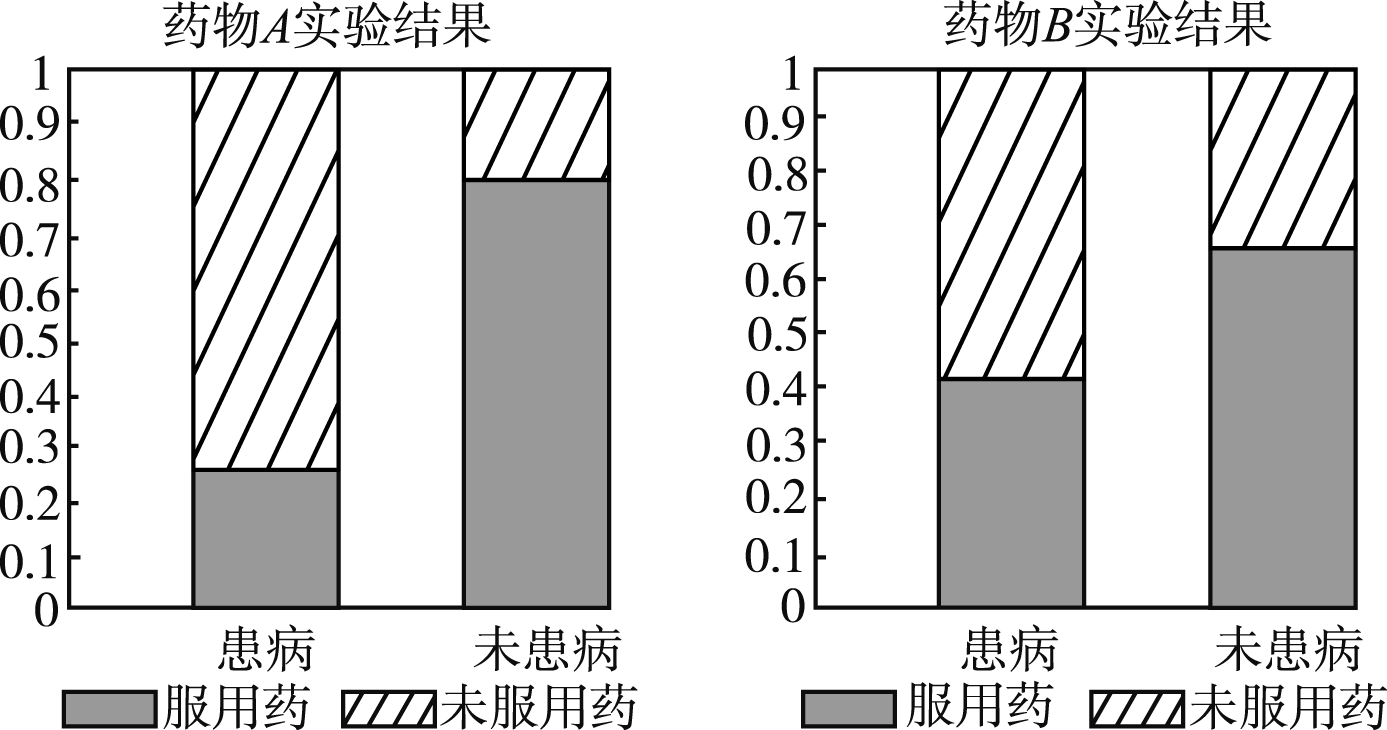
A.药物\(B\)的预防效果优于药物\(A\)的预防效果
B.药物\(A\)的预防效果优于药物\(B\)的预防效果
C.药物\(A,B\)对该疾病均有显著的预防效果
D.药物\(A,B\)对该疾病均没有预防效果
参考答案:B
A.8
B.9
C.8或9
D.6或8
参考答案:C
第150题
为了解高校学生使用手机支付和现金支付的情况,抽取了部分学生作为样本,统计其喜欢的支付方式,并制作出如下等高条形图: 根据图中的信息,下列结论中不正确的是( )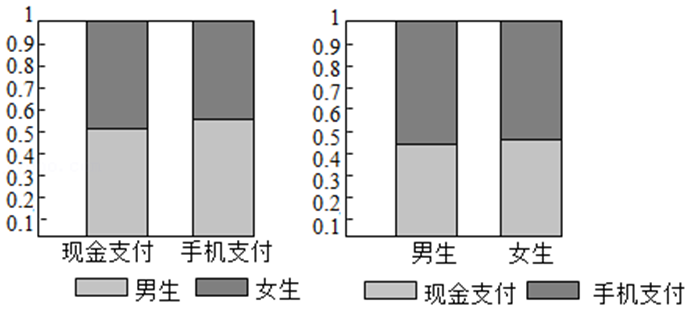
A.样本中的男生数量多于女生数量
B.样本中喜欢手机支付的数量多余现金支付的数量
C.样本中多数男生喜欢手机支付
D.样本中多数女生喜欢手机支付
参考答案:D
A.8
B.9
C.14
D.19
参考答案:C
A.若 \({\chi ^2} = 3.503\),当小概率值 \(\alpha = 0.1\) 时,推断 \({H_0}\) 不成立,即认为“秃顶与患心脏病有关联”
B.若 \({\chi ^2} = 3.503\),当小概率值 \(\alpha = 0.05\) 时,推断 \({H_0}\) 不成立,即认为“秃顶与患心脏病有关联”
C.若当小概率值 \(\alpha = 0.05\) 时推断 \({H_0}\) 不成立,即认为“秃顶与患心脏病有关联”,是说某人秃顶,那么他有 \(95\% \) 的可能性患心脏病
D.若当小概率值 \(\alpha = 0.1\) 时推断 \({H_0}\) 不成立,是指在犯错误的概率不大于0.1的前提下,认为“秃顶与患心脏病有关联”
参考答案:AD
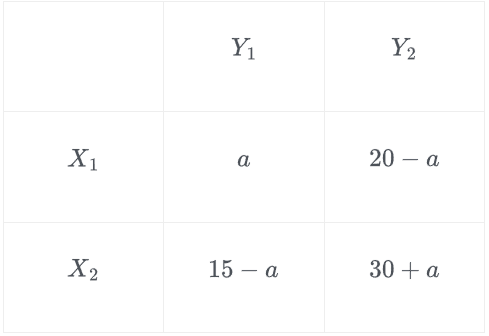
A.根据小概率值\(\alpha = 0.010\)的独立性检验,可以认为“阅读量多少与幸福感强弱无关”
B.\(m = 52\)
C.根据小概率值\(\alpha = 0.005\)的独立性检验,可以在犯错误的概率不超过0.5%的前提下认为“阅读量多少与幸福感强弱有关”
D.\(n = 42\)
参考答案:CD
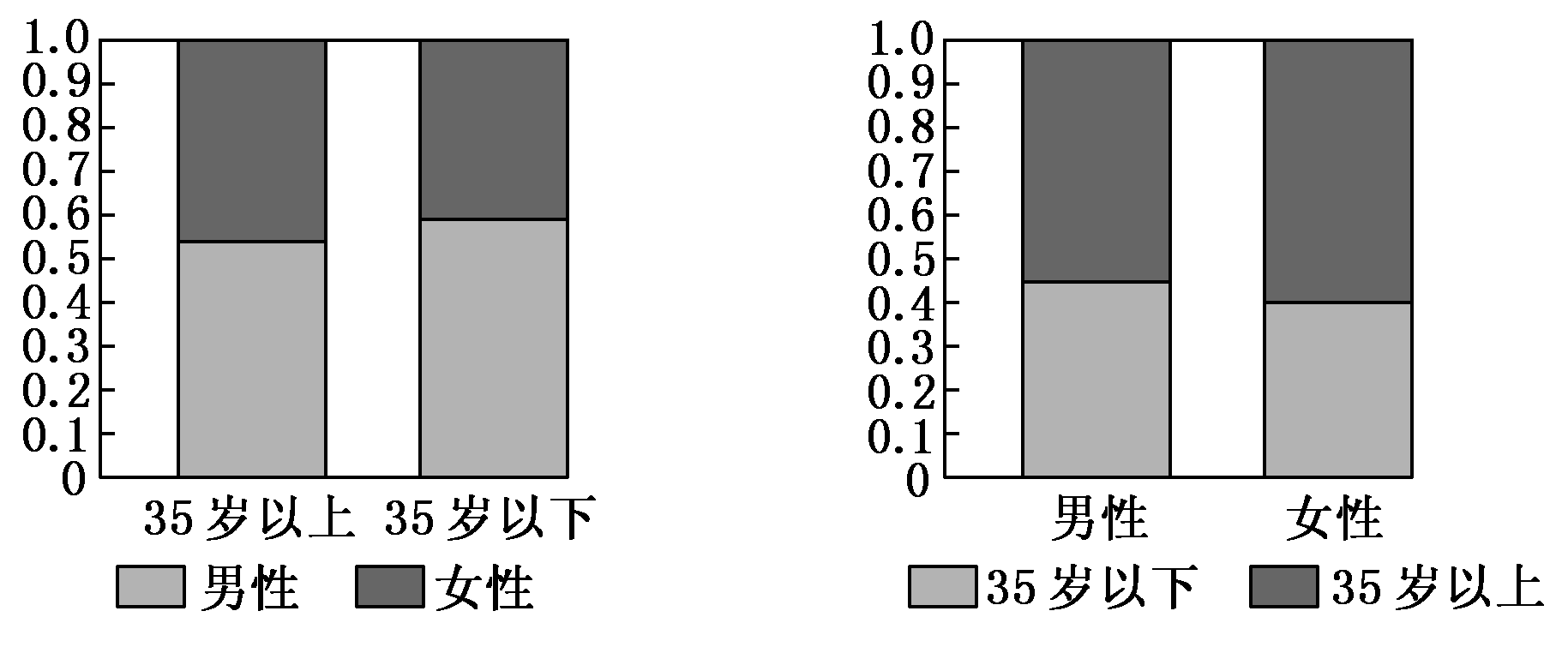
A.样本中男性比女性更关注地铁1号线全线开通
B.样本中多数女性是35岁以上
C.样本中35岁以下的男性人数比35岁以上的女性人数多
D.样本中35岁以上的人对地铁1号线的开通关注度更高
参考答案:ABD
参考答案:由已知吸烟总人数是 \(4 \div (1 - \frac{4}{5}) = 20\),因此吸烟患肺癌的人数是16,不吸烟的人数为20,不吸烟的人数中,患肺癌与不患肺癌的比为\(1:4\),则不吸烟的人数中,患肺癌与不患肺癌的人数分别是4和16,患肺癌的总人数是20,分层抽样的方法抽取\(5\)人,这5人中吸烟患肺癌的有4人,不吸烟患肺癌的有1人,吸烟患肺癌者的编号为\(a,b,c,d\),不吸烟患肺癌者的编号为1,从这5人中任抽取2人的基本事件有 \(ab,ac,ad,a1,bc,bd,b1,cd,c1,d1\) 共10个,2人均吸烟患肺癌的的事件有 \(ab,ac,ad,bc,bd,cd\) 共6个所求概率为 \(P = \frac{6}{{10}} = \frac{3}{5}\).
参考答案:由(1)得列联表为: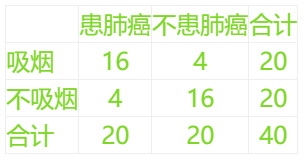
则\({\chi ^2} = \frac{{40 \times {{(16 \times 16 - 4 \times 4)}^2}}}{{20 \times 20 \times 20 \times 20}} = 14.4 > 10.828\),
所以能在犯错误概率不超过\(0.001\)的前提下,认为患肺癌与吸烟有关.
第160题
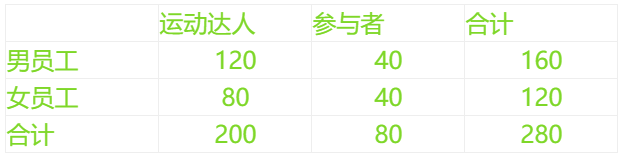
根据
参考答案:由列联表可得\({\chi ^2} = \frac{{280{{\left( {120 \times 40 - 40 \times 80} \right)}^2}}}{{200 \times 80 \times 160 \times 120}} \approx 2.333 < 2.706\),
所以没有\(90\% \)的把握认为获得“运动达人”称号与性别有关.