
“微信扫一扫”进入题库练习及模拟考试
高中数学 必修 第二册(415题)
为研究患肺癌与是否吸烟有关,做了一次相关调查,其中部分数据丢失,但可以确定的是不吸烟人数与吸烟人数相同,吸烟患肺癌人数占吸烟总人数的
在(1)的前提条件下,能不能在犯错误概率不超过
附:
其中

知识点:第七章 复数
参考答案:由(1)得列联表为: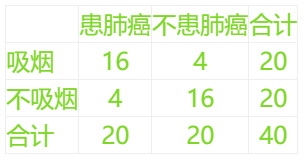
则\({\chi ^2} = \frac{{40 \times {{(16 \times 16 - 4 \times 4)}^2}}}{{20 \times 20 \times 20 \times 20}} = 14.4 > 10.828\),
所以能在犯错误概率不超过\(0.001\)的前提下,认为患肺癌与吸烟有关.