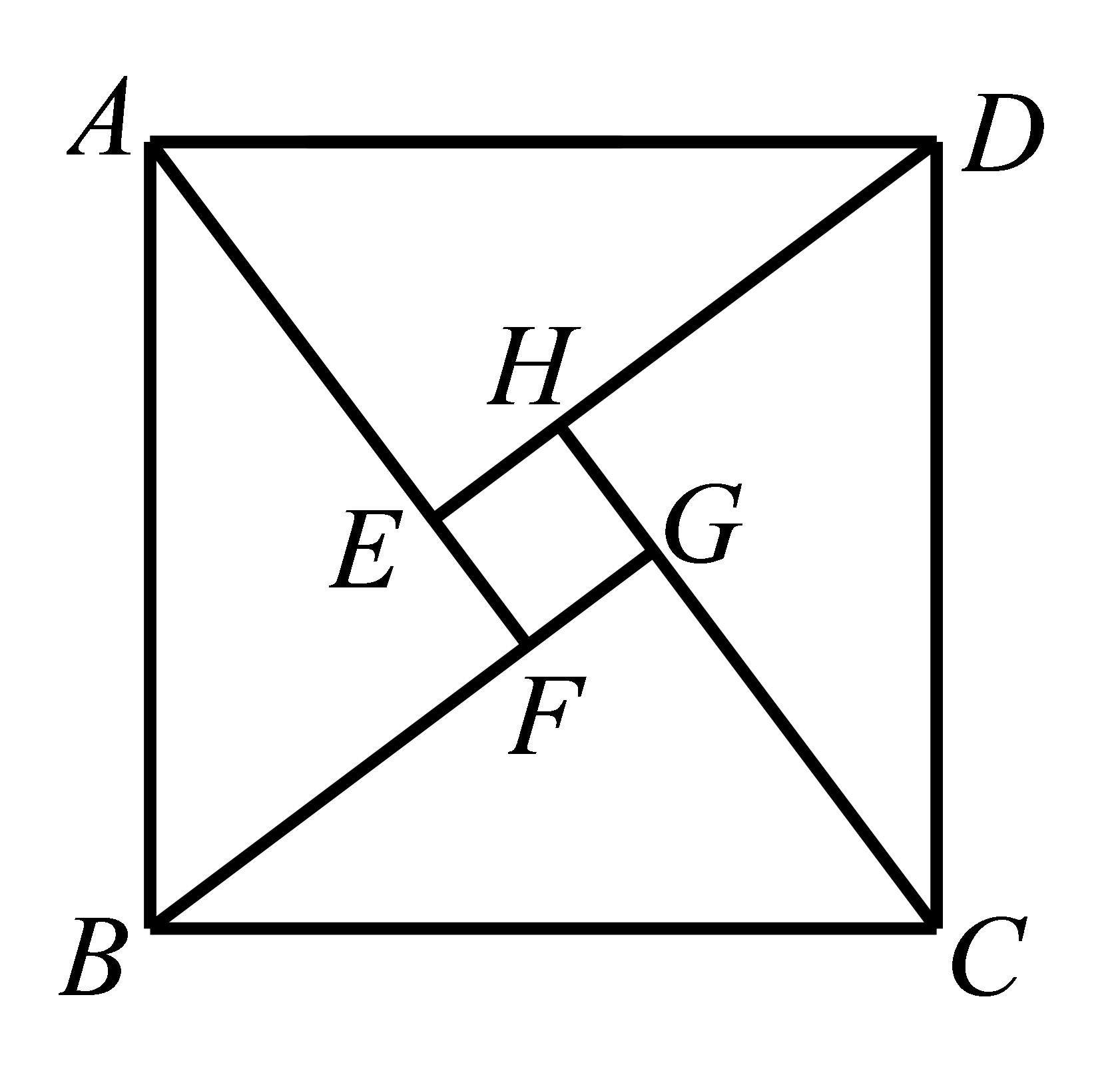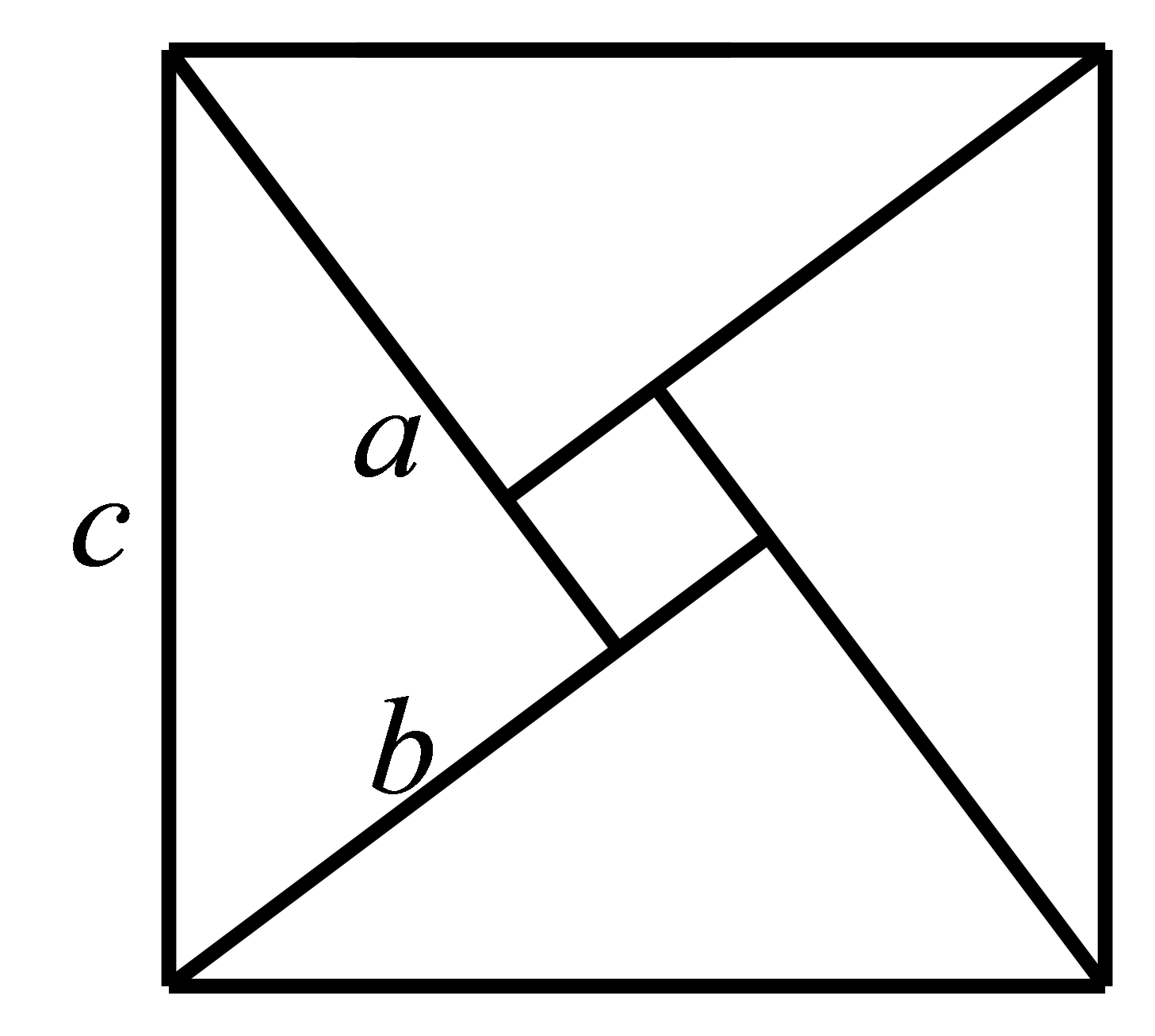“微信扫一扫”进入考试题库练习及模拟考试
初中数学八年级下册(648题)
参考答案:\( > , > , > , = \)
第184题
解答: 由(1)猜想\(a + b\)与\(2\sqrt {ab} \;(a \geqslant 0,b \geqslant 0)\)的大小关系,并说明理由.
参考答案:\(a + b \geqslant 2\sqrt {ab} \;(a \geqslant 0,b \geqslant 0)\)
第186题
证明:\({a_{n + 2}} = {a_n} + {a_{n + 1}}\).
参考答案:即证\(\frac{1}{{\sqrt 5 }}[{(\frac{{1 + \sqrt 5 }}{2})^{n + 2}} - {(\frac{{1 - \sqrt 5 }}{2})^{n + 2}}]
\)\(= \frac{1}{{\sqrt 5 }}[{(\frac{{1 + \sqrt 5 }}{2})^n} - {(\frac{{1 - \sqrt 5 }}{2})^n}] +
\)\( \frac{1}{{\sqrt 5 }}[{(\frac{{1 + \sqrt 5 }}{2})^{n + 1}} - {(\frac{{1 - \sqrt 5 }}{2})^{n + 1}}]\)
即\({(\frac{{1 + \sqrt 5 }}{2})^{n + 2}} - {(\frac{{1 - \sqrt 5 }}{2})^{n + 2}}
\)\(= {(\frac{{1 + \sqrt 5 }}{2})^n} - {(\frac{{1 - \sqrt 5 }}{2})^n} + {(\frac{{1 + \sqrt 5 }}{2})^{n + 1}} - {(\frac{{1 - \sqrt 5 }}{2})^{n + 1}}\),
即\({(\frac{{1 + \sqrt 5 }}{2})^n} \times {(\frac{{1 + \sqrt 5 }}{2})^2} - {(\frac{{1 - \sqrt 5 }}{2})^n} \times {(\frac{{1 - \sqrt 5 }}{2})^2}\)
\( = {(\frac{{1 + \sqrt 5 }}{2})^n} - {(\frac{{1 - \sqrt 5 }}{2})^n} +
\)\( {(\frac{{1 + \sqrt 5 }}{2})^n} \times (\frac{{1 + \sqrt 5 }}{2}) - {(\frac{{1 - \sqrt 5 }}{2})^n} \times (\frac{{1 - \sqrt 5 }}{2})\),
即\({(\frac{{1 + \sqrt 5 }}{2})^n} \times \left( {\frac{{3 + \sqrt 5 }}{2} - 1 - \frac{{1 + \sqrt 5 }}{2}} \right) -
\)\( {(\frac{{1 - \sqrt 5 }}{2})^n} \times \left( {\frac{{3 - \sqrt 5 }}{2} - 1 - \frac{{1 - \sqrt 5 }}{2}} \right) = 0\),
即\({(\frac{{1 + \sqrt 5 }}{2})^n} \times 0 - {(\frac{{1 - \sqrt 5 }}{2})^n} \times 0 = 0\),得证.
参考答案:9
A.①②
B.①②③
C.①②④
D.①②③④
参考答案:D
第194题
如图,点\(A\)在点\(O\)的北偏东30°的方向5 km处,\(AB⊥OA\).根据已知条件和图上尺规作图的痕迹判断,下列说法正确的是( )。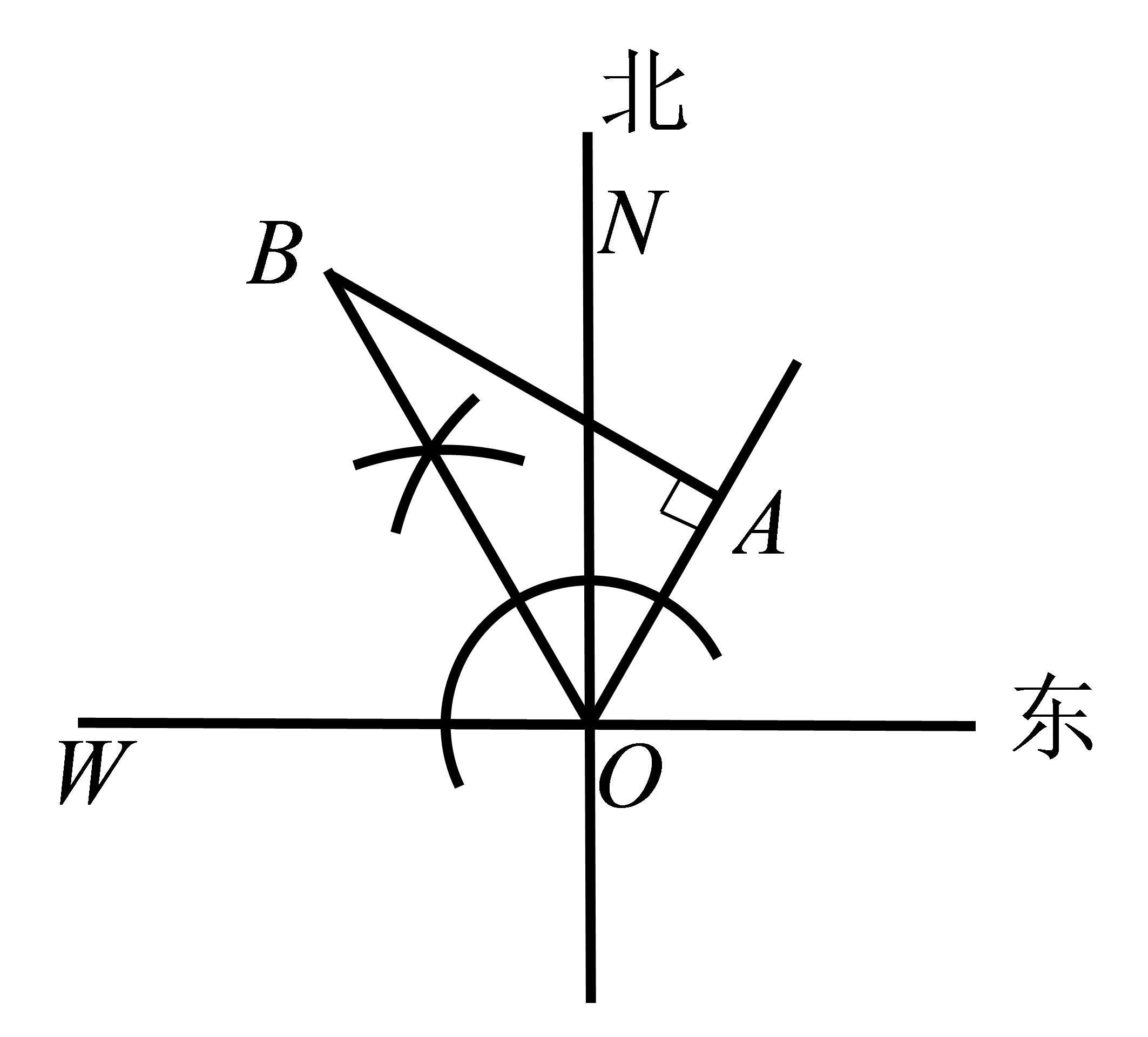
A.点\(B\)在点\(A\)的北偏西30°方向5 km处
B.点\(B\)在点\(A\)的北偏西60°方向5 km处
C.点\(B\)在点\(A\)的北偏西30°方向\(5\sqrt {3}\)km处
D.点\(B\)在点\(A\)的北偏西60°方向\(5\sqrt {3}\)km处
参考答案:D
参考答案:
由
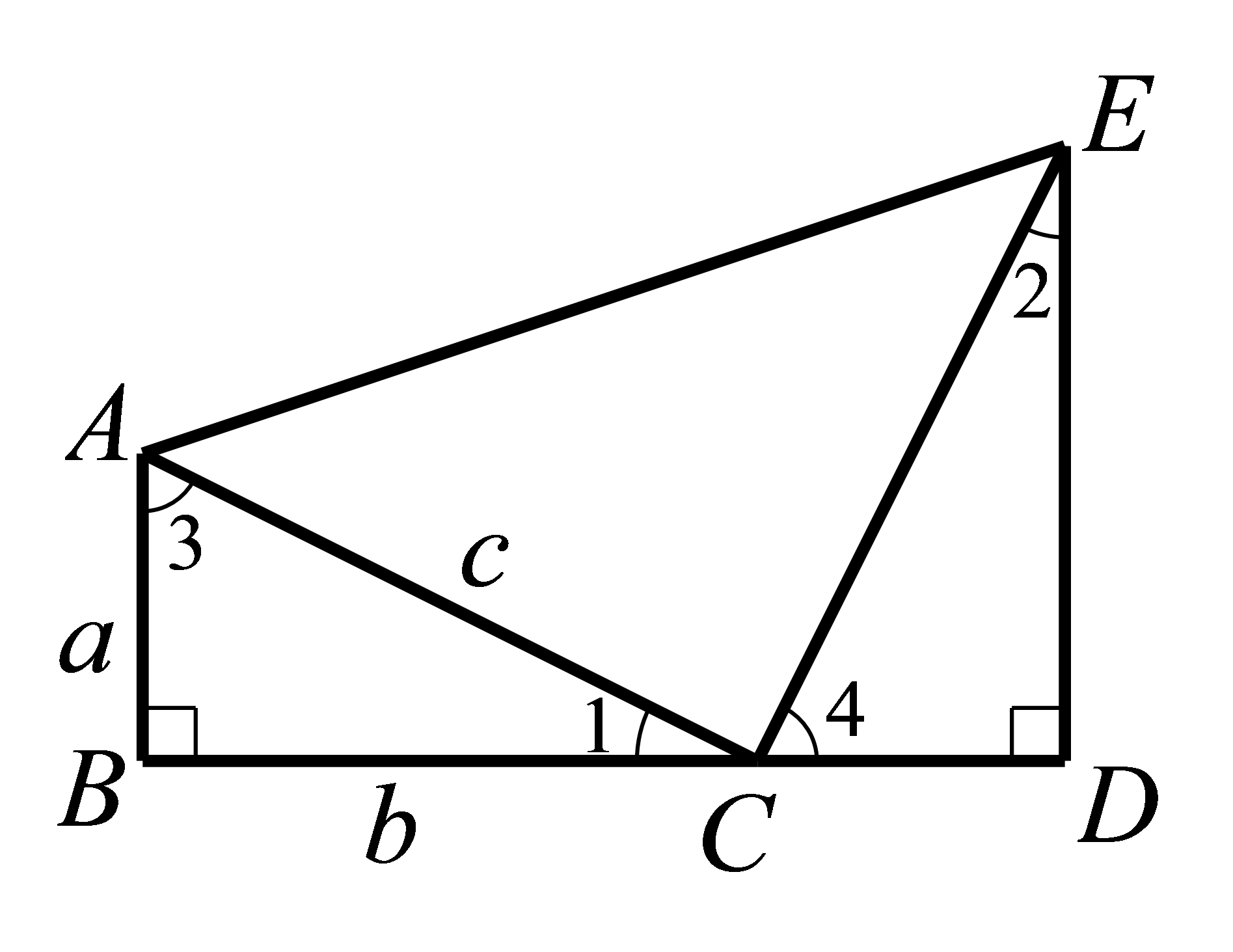
有
又
∴
A.24
B.30
C.40
D.50
参考答案:B