
“微信扫一扫”进入题库练习及模拟考试
初中数学八年级下册(648题)
如图,\(\text{Rt}△ABC≌\text{Rt}△CDE\),\(∠B=∠D=90°\),\(B、C、D\)三点在同一条直线上。 若\(AB=a,BC=b,AC=c\)。求证: \({a}^{2}+{b}^{2}={c}^{2}\)。
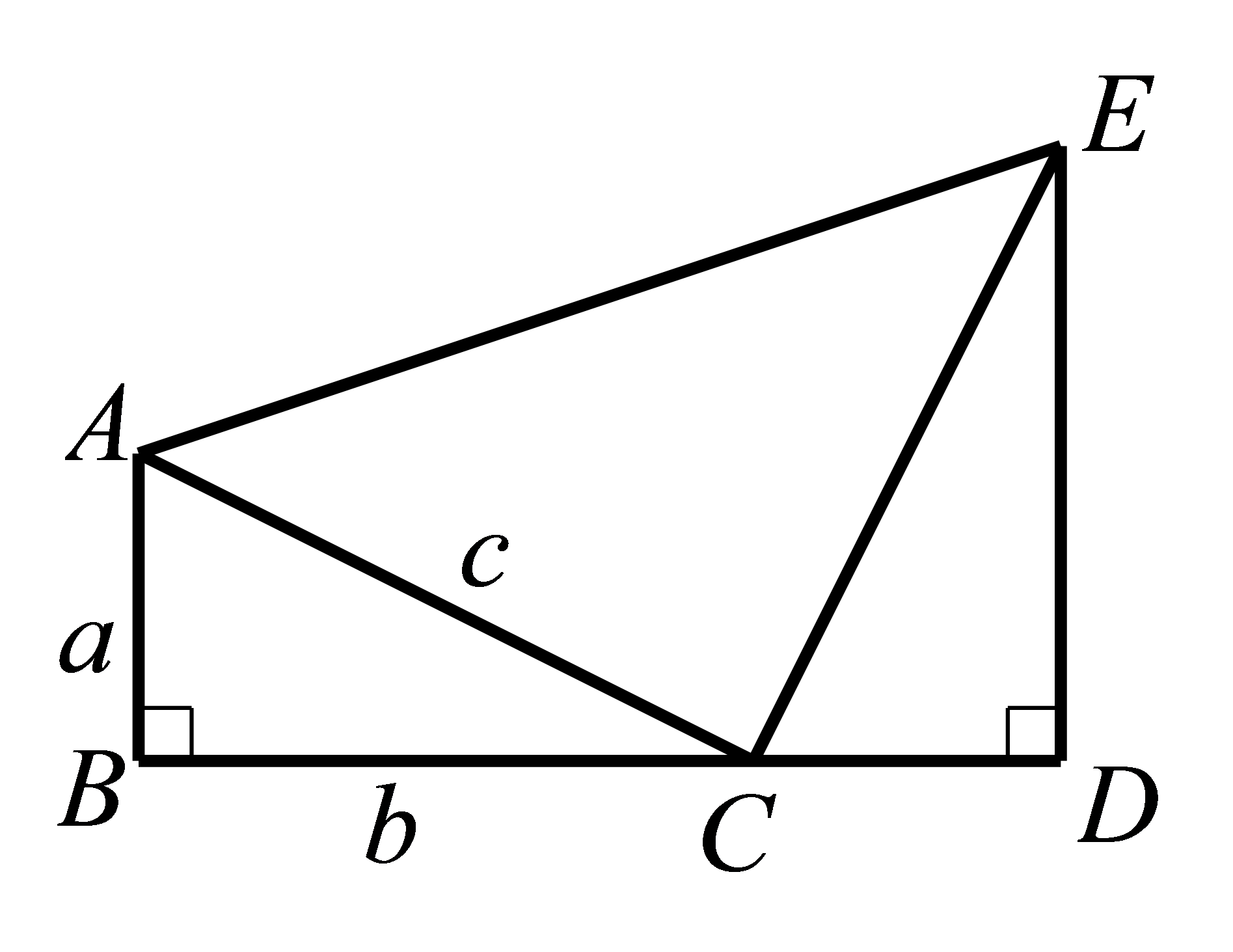
知识点:第十七章 勾股定理
参考答案:
由
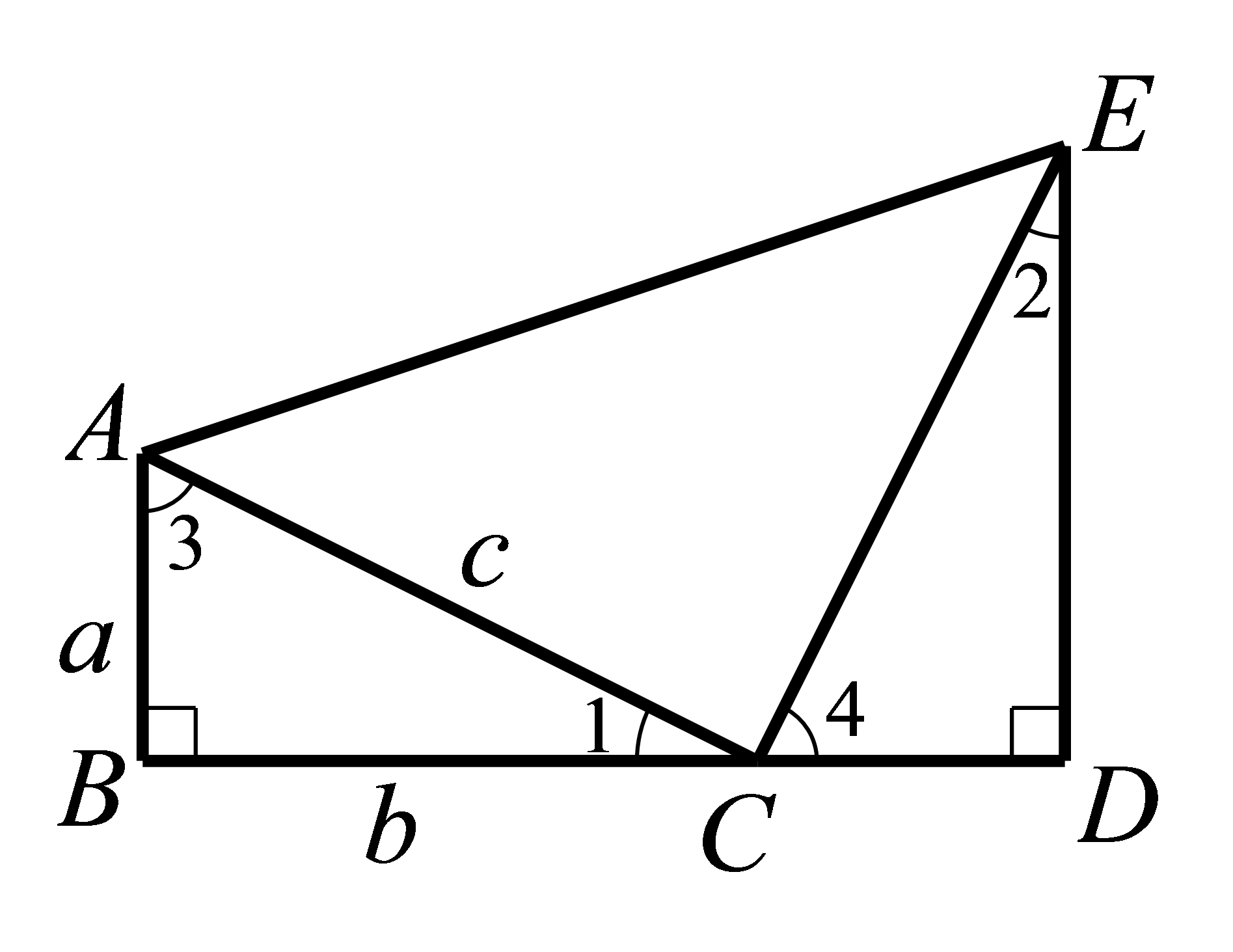
有
又
∴

“微信扫一扫”进入题库练习及模拟考试
如图,\(\text{Rt}△ABC≌\text{Rt}△CDE\),\(∠B=∠D=90°\),\(B、C、D\)三点在同一条直线上。 若\(AB=a,BC=b,AC=c\)。求证: \({a}^{2}+{b}^{2}={c}^{2}\)。
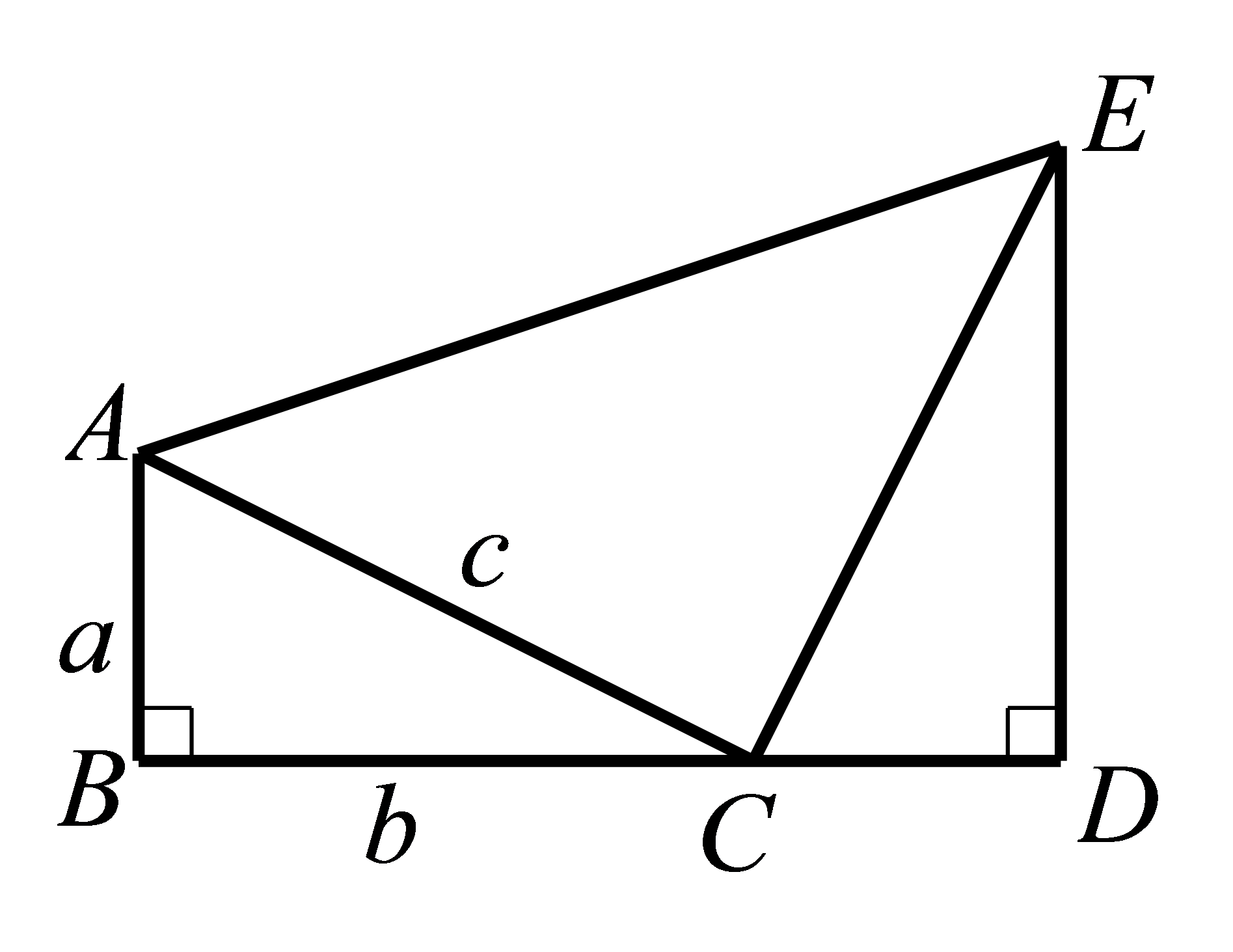
参考答案:
由
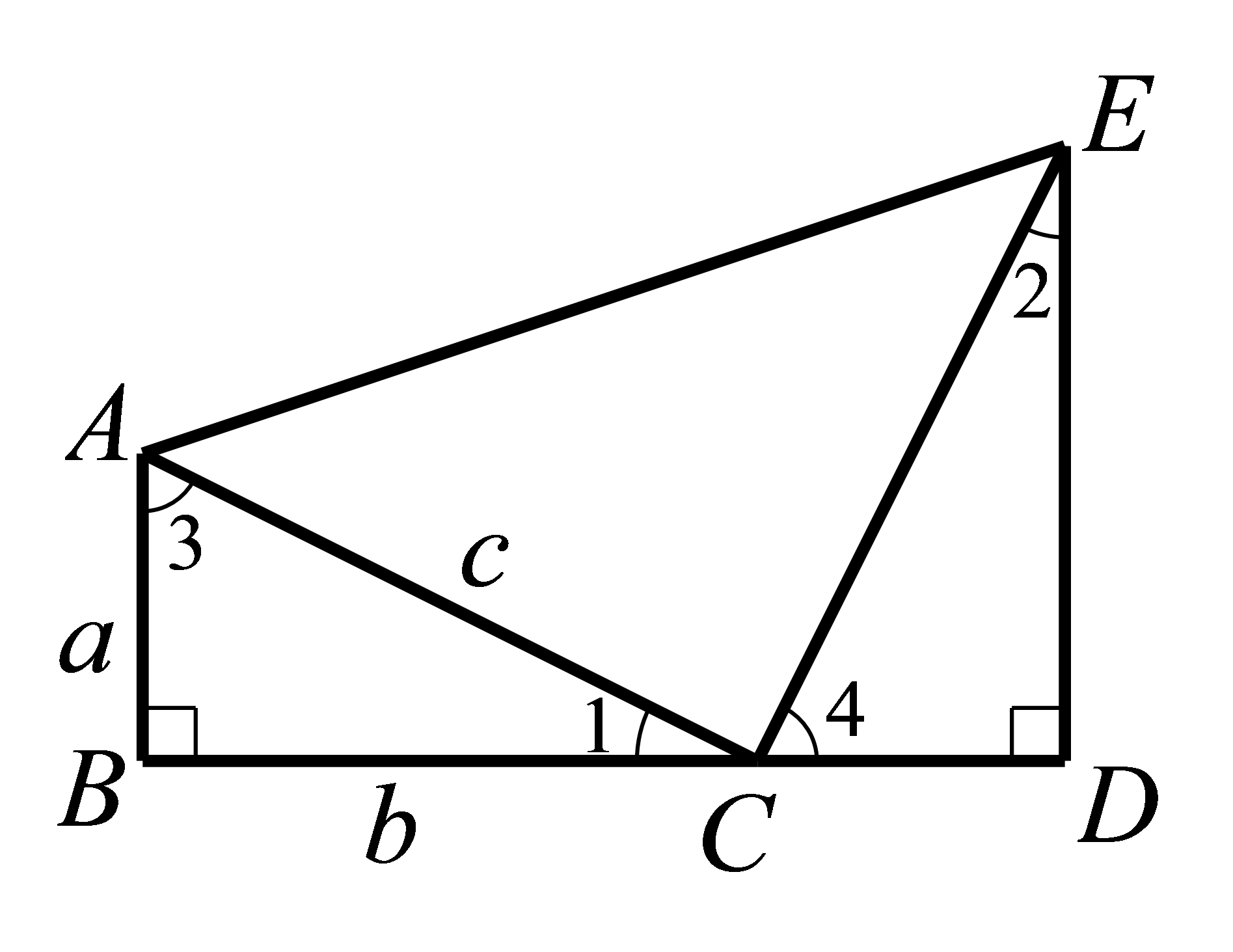
有
又
∴