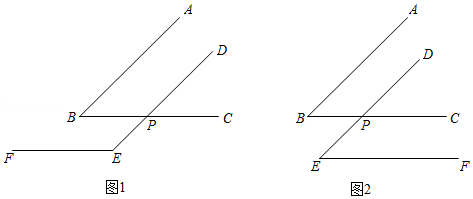“微信扫一扫”进入考试题库练习及模拟考试
初中数学七年级下册(573题)
第64题
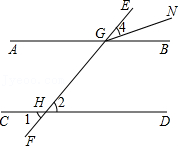
如图,直线\(AB//CD//EF\),点\(O\)在直线\(EF\)上,下列结论正确的是( )。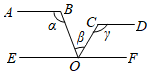
A.\(∠α+∠β-∠γ=90°\)
B.\(∠α+∠γ-∠β=180°\)
C.\(∠γ+∠β-∠α=180°\)
D.\(∠α+∠β+∠γ=180°\)
参考答案:B
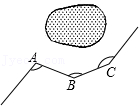
A.\(α-β\)
B.\(180°-β+α\)
C.\(360°-β-α\)
D.\(β-α\)
参考答案:B
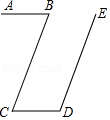
参考答案:\(∠ABC+∠DEF=180°\);\(∠ABC=∠DEF\)
如果两个角的两边互相平行,那么这两个角相等或互补。
30°,30°或70°,110°。
第68题
如图,一副三角板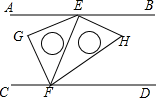
参考答案:27
A.\(360°\)
B.\(180°\)
C.\(250°\)
D.\(270°\)
参考答案:D
第71题
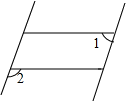
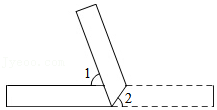
如图,将三角板与直尺贴在一起,使三角板的直角顶点\(C(∠ACB=90°)\)在直尺的一边上,若∠2=65°,则∠1的度数是( )。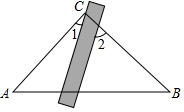
A.15°
B.25°
C.35°
D.65°
参考答案:B
第73题
试说明∠1=∠2;
参考答案:\(∵AB//CD,∴∠MEB=∠MFD\),
\(∵A'E//C'F\),
\(∴∠MEA'=∠MFC'\),
\(∴∠MEA'-∠MEB=∠MFC'-∠MFD\),
即∠1=∠2;
参考答案:由折叠知,\(∠C'FN\)\({\rm{ = }}\frac{{{{180}^ \circ }{\rm{ - }}\angle 2}}{2}{\rm{ = }}{70^ \circ }\),
\(∵A'E//C'F,∴∠A'EN=∠C'FN=70°\),
\(∵∠1=∠2\),
\(∴∠BEF=70°+40°=110°\)。
第76题
若
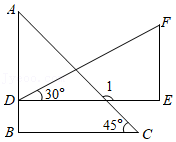
参考答案:\(∵DE//OB,∴∠O=∠ACE\),(两直线平行,同位角相等)
\(∵∠O=40°,∴∠ACE=40°\),
\(∵∠ACD+∠ACE=180°\),(平角定义)
\(∴∠ACD=140°\),
又\(∵CF\)平分\(∠ACD\),
\(∴∠ACF=70°\),(角平分线定义)
\(∴∠ECF=70°+40°=110°\)
第77题
求证:
参考答案:证明:\(∵CG⊥CF,∴∠FCG=90°\),
\(∴∠DCG+∠DCF=90°\),
又\(∵∠AOC=180°\),(平角定义)
\(∴∠GCO+∠FCA=90°\),
\(∵∠ACF=∠DCF,∴∠GCO=∠GCD\),(等角的余角相等)
即\(CG\)平分\(∠OCD\)。
第78题
当
参考答案:
结论:当
当
又
即
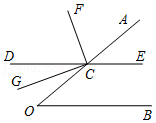
参考答案:对顶角的性质;两直线平行,同位角相等;\(\frac{1}{2}\);等量代换;\(\angle 4=\frac {1} {2}∠EGB\)