“微信扫一扫”进入考试题库练习及模拟考试
初中数学七年级下册(573题)
参考答案:\(∠EDF\);角平分线定义;\(∠EDF\);\(∠1=∠EDF\);\(DF//BE\)
第42题
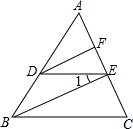
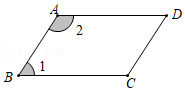
如图,\(∠CDA=∠CBA\),\(DE\)平分\(∠CDA\),\(BF\)平分\(∠CBA\),且\(∠ADE=∠AED\),证明:(1)\(AB//CD\)(2)\(DE//BF\)。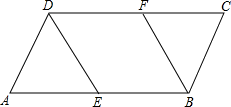
参考答案:(1)\(∵DE\)平分\(∠CDA\),
\(∴∠ADE=∠EDC\),
而\(∠ADE=∠AED\),
\(∴∠EDC=∠AED,∴AB//CD\);
(2)\(∵BF\)平分\(∠CBA\),
\(∴∠ABF=\frac {1} {2}∠ABC\),
\(∵∠AED=∠ADE=\frac {1} {2}∠ADC\),
而\(∠CDA=∠CBA\),
\(∴∠AED=∠ABF,∴DE//BF\).
参考答案:\(AB//CD\)
第45题
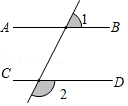
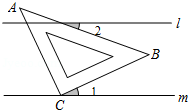
如图,直线\(a、b\)被直线\(c\)所截,下列条件不能判定直线\(a\)与\(b\)平行的是( )。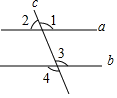
A.\(∠1=∠3\)
B.\(∠2+∠4=180°\)
C.\(∠1=∠4\)
D.\(∠1+∠4=180°\)
参考答案:D
第47题
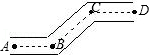
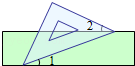
如图,将木条\(a,b\)与\(c\)钉在一起,\(∠1=75°,∠2=45°\),要使木条\(a\)与\(b\)平行,木条\(a\)旋转的度数至少是( )。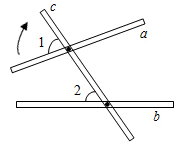
A.15°
B.25°
C.30°
D.50°
参考答案:C
参考答案:已知;角平分线的定义;2∠β;角平分线的定义;∠α+∠β;180°;同旁内角互补,两直线平行
第51题
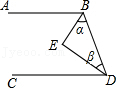
如图,下列条件中: ①\(∠B+∠BCD=180°\); ②\(∠1=∠2\); ③\(∠3=∠4\); ④\(∠B=∠5\); 则一定能判定\(AB//CD\)的条件有___(填写所有正确的序号)。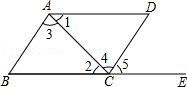
参考答案:①③④
第55题
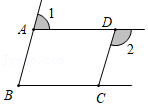
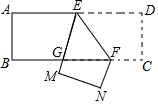
如图,\(ABCD\)为一长条形纸带,\(AB//CD\),将\(ABCD\)沿EF折叠,\(A、D\)两点分别与\(A'、D'\)对应,若\(∠1=2∠2\),则\(∠AEF\)的度数为( )。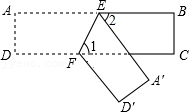
A.60°
B.65°
C.72°
D.75°
参考答案:C
第57题
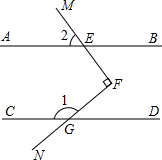
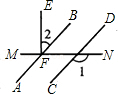
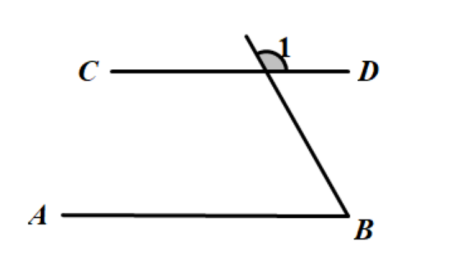
如图,\(AB//CD\),\(∠BEC\)的平分线交\(CD\)于点\(F\),若\(∠MEB=52°\),求\(∠EFC\)的度数。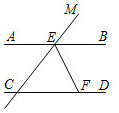
参考答案:\(∵∠MEB=52°\),
\(∴∠BEC=180°-52°=128°\);
\(∵EF\)平分\(∠BEC\),
\(∴∠BEF=\frac {1} {2}∠BEC=64°\);
又\(∵AB//CD\),
\(∴∠EFC=∠BEF=64°\)
第58题
已知:如图,\(EF\)平分\(∠DEB\),\(AC//DE,CD//EF\),请证明:\(CD\)平分\(∠ACB\)。
参考答案:\(∵AC//DE,∴∠ACD=∠CDE\),
\(∵CD//EF,∴∠DCB=∠FEB,∠CDE=∠DEF\),
\(∴∠ACD=∠DEF\),
又\(∵EF\)平分\(∠DEB\),
\(∴∠DEF=∠FEB\),
\(∴∠ACD=∠DCB\),
\(∴CD\)平分\(∠ACB\)。
参考答案:
如图1,过点
 ,
,
又
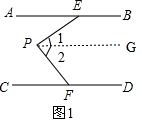
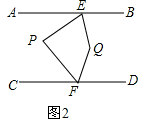
第60题 在图2中,画\(∠BEP\)的平分线与\(∠DFP\)的平分线,两条角平分线交于点\(Q\),请你补全图形,试探索\(∠EPF\)与\(∠EQF\)之间的关系,并证明你的结论。
参考答案:
如图2,
 ,
,
由(1)可得: