第181题

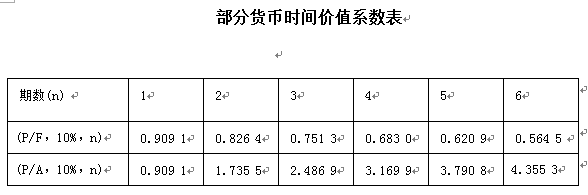
在利率为10%的条件下，一至三年期的复利现值系数分别为0.9091,0.8264,0.7513，则三年期的年金现值系数为(    )。

A.2.4868

B.1.7355

C.0.7513

D.2.7355

参考答案：A

解析：

年金现值系数是每次收支的复利现值系数之和，即(P/A,10%，3)=(P/F，10%,1)+(P/F,10%,2)+(P/F,10%,3)=0.9091+0.8264+0.7513=2.4868。

第182题

张先生准备2019年年初购买一套新房，开发商提供了四种付款方案让张先生选择：
（1）A方案，从第4年年末开始支付，每年年末支付20万元，一共支付8年；
（2）B方案，每年年初支付15万元，一共支付10年；
（3）C方案，从第4年年初开始支付，每年支付19万元，一共支付8年。

（4）D方案，2022年初一次性支付130万元
假设所有的款项均需要靠银行贷款解决，银行贷款年利率为5%。
已知：（P/F，5%，2）＝0.9070，（P/F，5%，3）＝0.8638
（P/A，5%，8）＝6.4632，（P/A，5%，10）＝7.7217

（结果保留两位小数）

要求：
（1）计算A方案的付款现值；
（2）计算B方案的付款现值；
（3）计算C方案的付款现值；

（4）计算D方案的付款现值；
请问张先生应该选择哪种方案。

参考答案：见解析

解析：

（1）A方案付款的现值＝20×（P/A，5%，8）×（P/F，5%，3）＝20×6.4632×0.8638＝111.66（万元）
（2）B方案付款的现值＝15×（P/A，5%，10）×(1+5%)＝15×7.7217×1.05＝121.62（万元）
（3）C方案付款的现值＝19×（P/A，5%，8）×（P/F，5%，2）＝19×6.4632×0.9070＝111.38（万元）

（4）D方案付款的现值=130×（P/F，5%，3）=130×0.8638=112.29（万元）

由于C方案付款的现值最小，所以张先生应该选择C方案。

第183题

计算方案一的现值。

参考答案：见解析

解析：复利求现值，i=10%，n=2。

第184题

计算方案二的现值。

参考答案：见解析

解析：预付年金求现值，预付年金现值=普通年金现值×（1＋i），i=10%，n=3。

第185题

计算方案三的现值。

参考答案：见解析

解析：普通年金求现值，第一笔现金流在2019年初，即2018年末（第一期期末开始等额收付的系列款项），i=10%，n=4。

第186题

计算方案四的现值。

参考答案：见解析

解析：递延年金求现值，2020年初（即2019年年末），是从第二期期末（即2时点）开始等额收付的系列款项。在第一笔现金流量（2时点）的前一期（1时点）划分界限，因此递延期m=1，n=5，i=10%。带入公式，递延年金现值：P=A× （P/A，i，n）×（P/F，i，m）。

第187题

判断甲公司应选择哪种付款方案。

参考答案：见解析

解析：

因为方案四的现值最小，所以甲公司应选择方案四的付款方案。

第188题

下列关于资金时间价值系数关系的表述中，正确的有（　）。

A.预付年金现值系数＝普通年金现值系数×（1＋i）

B.复利终值系数和复利现值系数互为倒数关系

C.年金终值系数和年金现值系数互为倒数关系

D.预付年金终值系数＝普通年金终值系数×（1＋i）

参考答案：ABD

解析：

年金终值系数和年金现值系数不是互为倒数的关系。年金终值系数与年偿债基金系数互为倒数，年金现值系数与年资本回收系数互为倒数。所以第3个选项的表述错误。

第189题

某公司需要在10年内每年等额支付100万，年利率为i，如果在每年年末支付，全部付款额的现值为X，如果在每年年初支付，全部付款额的现值为Y，则Y和X的数量关系可以表示为（）

A.Y=X/（1+i）-i

B.Y=X/（1+i）

C.Y=X（1+i）-1

D.Y=X（1+i）

参考答案：D

解析：

预付年金现值Y=普通年金现值X*（1+i），所以选项D正确。

第190题

某投资项目于2012年年初动工，假设当年投产，从投产之日起每年年末可得收益40000元。按年折现率6%计算（复利计息），计算预期10年收益的现值（   ）  年金现值系数：（P/A，6%，10）=7.3601

参考答案：见解析

解析：

P＝40000×（P/A，6%，10）＝40000×7.3601＝294404（元）

第191题

预付年金与普通年金的区别在于年金发生的时间不同。(       )

参考答案：对

第192题

甲公司于2018年1月1日购置一条生产线，有四种付款方案可供选择。

方案一：2020年初支付100万元。

方案二：2018年至2020年每年初支付30万元。

方案三：2019年至2022年每年初支付24万元。

方案四：2020年至2024年每年初支付21万元。

公司选定的折现率为10%，部分货币时间价值系数如下表所示。

要求：

（1）计算方案一的现值。

（2）计算方案二的现值。

（3）计算方案三的现值。

（4）计算方案四的现值。

（5）判断甲公司应选择哪种付款方案。

参考答案：见解析

解析：

（1）方案一的现值：100×（P/F,10%，2）=100×0.8264=82.64（万元）

（2）方案二的现值：30+30×（P/A,10%，2）=30+30×1.7355=82.07（万元）

（3）方案三的现值：24×（P/A,10%，4）=24×3.1699=76.08（万元）

（4）方案四的现值：21×（P/A,10%，5）×（P/F,10%，1）=21×3.7908×0.9091=72.37（万元）

（5）甲公司应该选择方案四。

第193题

下列各项中，属于普通年金形式的项目有(    )。

A.零存整取储蓄存款的整取额

B.定期定额支付的养老金

C.年资本回收额

D.偿债基金

参考答案：BCD

解析：

年金是指一定时期内每次等额收付的系列款项，通常记作A。年金的形式包括:保险费/养老金/折旧/租金/等额分期收款/零存整取或整存零取储蓄等。零存整取储蓄存款的整取额应该属于年金终值，不属于年金。

第194题

已知（F/P，9%，4）＝1.4 116，（F/P，9%，5）＝1.5 386，（F/A，9%，4）＝4.5 731，则（F/A，9%，5）为（    ）。

A.4.9 847

B.5.9 847

C.5.5 733

D.4.5 733

参考答案：B

解析：

（F/A，9%，5）＝（F/A，9%，4）×（1＋9%）＋1＝4.5 731×（1＋9%）＋1＝5.9 847，选项B正确。

第195题

每年年初存款，第10年末获得500万元，利率7%，复利计算，每年存（）

A.500/[(F/A,7%,11)-1]

B.500/[(F/A,7%,9)*(1+7%)]

C.500/[(F/A,7%,11)/(1+7%)]

D.500/[(F/A,7%,9)+1]

参考答案：A

解析：

500=A*[(F/A,7%,10)*(1+7%)]，因此A=500/[(F/A,7%,10)*(1+7%)]，选项B、C错误。或者：500=A*[(F/A,7%,11)-1]，因此A=500/[(F/A,7%,11)-1]，选项A正确、选项D错误。

第196题

已知（F/P，9％，4）=1.4116，（F/P，9%，5）=1.5386,（F/A，9%，4）=4.5731，则（F/A，9％，5）为（   ）。

A.4.9847

B.5.9847

C.5.5733

D.4.5733

参考答案：B

解析：

对于等额收付n次的普通年金而言，其终值指的是各期等额收付金额在第n期期末的复利终值之和。计算普通年金终值的一般公式为：=A+A（1+i）+A（1+i）²+…+A（1+i）n–1。

令A=1，则：F1=1×（F/A，9%，5）=1+（1+9%）+（1+9%）²+（1+9%）³+（1+9%）⁴，

F0=1×（F/A，9%，4）=1+（1+9%）+（1+9%）²+（1+9%）³

因此，（F/A，9%，5）=（F/A，9%，4）+（F/P，9%，4）=4.5731+1.4116=5.9847。

或

方法一：（F/A，9％，5）=（F/A，9％，4）×（1+9％）+1=5.9847。

方法二：（F/A，9％，5）=（F/A，9％，4）+（F/P，9％，4）=4.5731+1.4116=5.9847

第197题

已知（P/A，8%，5）＝3.9927，（P/A，8%，6）＝4.6229，则6年期、折现率为8%的预付年金现值系数是（　    ）。

A.2.9927

B.4.2064

C.4.9927

D.6.2064

参考答案：C

解析：

本题考查预付年金现值系数与普通年金现值系数的关系。即预付年金现值系数等于同利率同期数普通年金现值系数乘（1+i），所以6年期折现率为8%的预付年金现值系数＝（P/A，8%，6）×（1+8%）＝4.6229×1.08＝4.9927。

第198题

A公司拟购置一处房产，房主提出两种付款方案：

方案一：从现在起，每年年初支付200万元，连续付10次，共2000万元

方案二：从第5年开始，每年年初支付250万元，连续支付10次，共2500万元。

假设该公司的资本成本率（即最低收益率）为10%，你认为A公司应选择哪个方案？

（P/A，10%，10）=6.1446，（P/F，10%，3）=0.7513

参考答案：见解析

解析：

【解题思路】方案一为预付年金，方案二为递延年金，由于第1次支付发生在第5期期初（相当于第4期期末），所以，递延期为3，由于连续支付10次，所以n=10。计算两个方案的现值进行决策，由于是付款方案，所以现值最小的方案最优。

方案一：P₀=200×（P/A，10%，10）×（1+10%）=1351.81（万元）

方案二：P₀=250×（P/A，10%，10）×（P/F，10%，3）=1154.11（万元）

决策：方案二的现值较小，A公司应该选择方案二。

第199题

甲公司打算购买一台设备，有两种付款方式：一是一次性支付500万元，二是每年初支付200万元，3年付讫。由于资金不充裕，公司计划向银行借款用于支付设备款。假设银行借款年利率为5%，复利计息。请问甲公司应采用哪种付款方式？（P／A，5%，3）=2.7232

参考答案：见解析

解析：

方案一：现在一次性支付500万元

方案二：计算预付年金现值：

 P=A×（P／A，i，n）×（1＋i）=200×（P／A，5%，3）×（1＋5%）=200×2.7232×1.05=571.87（万元）

决策：因为方案一现值（500万元）小于方案二现值（571.87万元），甲公司应采用第一种支付方式。

第200题

6年分期付款购物，每年年初付款500元，设银行利率为10%，该项分期付款相当于现在一次现金支付的购价是(       )。

(P/A,10%,6)=4.3553;(P/A,10%,7)=4.8684;(P/A,10%,5)=3.7908.

A.2395.40元

B.1895.40元

C.1934.40元

D.2177.40元

参考答案：A

解析：

本题考核预付年金现值的计算。预付年金现值=年金额×预付年金现值系数(普通年金现值系数表期数减1系数加1)=500×(P/A,10%,6)*(1+10%)=2395.4(元)。