第521题 某水果经销商到一山区水果基地采购猕猴桃和苹果。猕猴桃和苹果的采购价分别为10元/斤和4元/斤,销售价分别为25元/斤和12元/斤。已知该经销商在本次经销中获利40000元,每种水果采购都超过500斤且为整数。问该经销商的最佳投入资金是多少元?

A.20000

B.21260

C.21300

D.21280

参考答案：B

解析：

第一步，本题考查基础应用题，用方程法解题。

第二步，设猕猴桃、苹果分别购买的重量为x 斤、y 斤，由题意可得：（25-10）x＋（12-4）y=40000，化简为15x+8y=40000。根据数字特性可知，x 为8 的倍数；又因x 要最少（投入最少）且大于500，则x=504，y=4055。则最佳投入为504×10+4055×4=21260（元）。

因此，选择B 选项。

第522题 同事甲、乙两人共携带120千克行李乘坐飞机,根据规定,甲单独托运则超重需支付200元,乙单独托运则超重需支付100元。若全部行李由一人负责托运,则超重需支付450元。问每位乘客的免费托运的行李最多为多少千克?

A.20

B.25

C.30

D.35

参考答案：C

解析：

解法一：

第一步，本题考查基础应用题，用方程法解题。

第二步，除去免费行李重量，甲比乙多付100 元，两人合计300 元，那么当一人托运时多支付的450-300=150（元）就是免费重量转为非免费的支付费用。设免费重量为x 千克，超出的部分为n 元/千克，由题意有：①nx=150，②（120-x）n=450，联立两式解得x=30，n=5。

因此，选择C 选项。

解法二：

第一步，本题考查基础应用题，用数字特性法解题。

第二步，支付的钱数=重量×单价，乙付的钱不是3 的倍数，而合计支付的钱是3 的倍数，可知合计支付中的重量是3 的倍数；而合计支付重量+免费重量=总重量，总重量120 千克也是3 的倍数，则免费重量应该也是3 的倍数。只有C 符合。

因此，选择C 选项。

第523题 小李一家3人进行抢红包游戏,每人发1个红包。结果每人抢得金额总额一致,均为100元,刚巧3人所发红包金额为互不相同整数且成等差数列。问3人中所发红包金额最多的可能是多少元?

A.197

B.198

C.199

D.200

参考答案：C

解析：

解法一：

第一步，本题考查数列问题。

第二步，每人抢到的红包金额为100 元可知三人所发红包总金额为300 元，且金额第二多的红包即平均数100 元。那么想要最大的红包面额最多，需要最小的红包面额最小，最小为1 元，那么最大为300-100-1=199（元）。

因此，选择C 选项。

解法二：

第一步，本题考查数列问题，用代入排除法求解。

第二步，题目问最大，优先代入200 元。由等差数列性质可知金额第二多的红包即平均数100 元，假如最大红包是200 元，则公差为100 元，最小的红包是0 元，无法发出红包；假如最大红包是199 元，则公差为99 元，最小的红包是1 元，符合题意。

因此，选择C 选项。

第524题 春节期间,省图书馆邀请多位书法老师免费为读者书写春联。现场书写的春联中有188幅不是A老师书写的,有219幅不是B老师书写的,A、B两位老师今年一共书写了311幅春联。 问B老师今年一共书写了多少幅春联?

A.208

B.171

C.140

D.126

参考答案：C

解析：

解法一：

第一步，本题考查基础应用题，用方程法求解。

第二步，由题干“现场书写的春联中有188 幅不是A 老师书写的，有219 幅不是B 老师书写的”，可知A 老师比B 老师多书写了219-188=31（幅）。设B 老师书写了x 幅春联，则A 老师书写了x+31 幅春联，由题意有x+（x+31）=311，解得x=140。

因此，选择C 选项。

解法二：

第一步，本题考查基础应用题，用代入排除法求解。

第二步，根据就简代入原则，优先代入C 选项140 验证。则今年总共书写了140+219=359（幅）春联，A 老师书写了359-188=171（幅）春联，A，B 两位老师今年一共书写了140+171=311（幅）春联，完全符合题意。

因此，选择C 选项。

第525题 从某物流园区开出6辆货车,这6辆货车的平均装货量为62吨,已知每辆货车载重量各不相同且均为整数,最重的装载了71吨,最轻的装载了54吨。问这6辆货车中装货第三重的卡车至少装载了多少吨?

A.59

B.60

C.61

D.62

参考答案：B

解析：

第一步，本题考查最值问题，属于数列构造。

第二步，总和一定，求某项最值，使用数列构造的方法。首先，根据题意将6 辆货车的的载重量从大到小排序则第一重的为71 吨，最轻的为54 吨，求第三重的卡车至少载重多少，则其余货车载重尽量多，所以构造排名第二至第五的载重依次为：70，x，x－1，x－2。求和有：71＋70＋x＋（x－1）＋（x－2）＋54＝62×6，解得x＝60。

因此，选择B 选项。

第526题 甲、乙两人同时加工一批零件,速度比为3：2,当两人共同完成总任务的一半后,甲生产速度降低20%,乙生产速度提高20%,当甲完成总任务的一半时,还剩100个零件未加工,问这批零件总数在以下哪个范围内?

A.不到500

B.500~800

C.801~1200

D.超过1200

参考答案：C

解析：

第一步，本题考查工程问题，属于效率类，用赋值法解题。

第二步，根据甲乙速度比为3∶2，赋值甲乙的效率分别为3 和2，设工程总量为10x，当两人共同完成总任务的一半时，甲完成了3x、乙完成了2x，之后甲的速度变为3×（1-20%）=2.4、乙的速度变为2×（1+20%）=2.4，当甲完成总量的一半时，甲又完成了2x，由于甲乙效率相同，乙也完成了2x，此时还剩x 的工作量为100 个零件，这批零件总数为10x=1000（个）。

因此，选择C 选项。

第527题 某景区圆形摩天轮,最高点距离地面120米,旋转半径50米。摩天轮开启后按逆时针方向旋转,旋转一周大约需 30分钟,甲在最低点的位置坐上摩天轮,则第45分钟时甲距离地面大约多少米?

A.45

B.70

C.100

D.120

参考答案：D

解析：

第一步，本题考查几何问题，属于平面几何类。

第二步，由旋转一周大约需30 分钟，则45 分钟时旋转一周半。甲在最低点位置坐上，旋转一周半到摩天轮最高
点，摩天轮最高点距离地面120 米，甲距离地面120 米。

因此，选择D 选项。

第528题 某单位开展“我身边的榜样”评选活动,现对3名候选人甲、乙、丙进行不记名投票,投票要求详见选票。这3名候选人的得票数(不考虑是否有效)分别为总票数的88%、70%、46%,则本次投票的有效率(有效票数与总票数的比值)最高可能为：

A.68%

B.88%

C.96%

D.98%

参考答案：C

解析：

第一步，本题考查最值问题，属于其他最值构造。

第二步，设总共有100 人投票，则共出现了88+70+46=204（次），每张选票的个数不超过2 时才为有效票，先每张选票分2 个，此时还剩4 个，则无效票最少有4 张，本次投票的有效率最高可能为96%。

因此，选择C 选项。

第529题 疫情期间,某地推出电子健康码,用户需凭电子健康码出入小区、学校、医院等公共场所。健康码是黑白相间的二维码,该二维码是边长为15cm的正方形,现利用随机模拟的方法向该健康码内投入1500个点,其中落入黑色部分的点的个数为800个,则该健康码的黑色部分的面积约为多少cm²?

A.135

B.120

C.115

D.105

参考答案：B

解析：

第一步，本题考查几何问题，属于平面几何类。

第二步，利用正方形的面积= =15×15=225（cm²），黑色面积占总面积的，面积=225× =120（cm²）。

因此，选择B 选项。

第530题 学校有300个学生选择参加地理兴趣小组,生物兴趣小组或者两个小组同时参加。如果80%学生只参加地理兴趣小组,50%学生只参加生物兴趣小组。问同时参加地理和生物兴趣小组的学生人数是多少?

A.240

B.150

C.90

D.60

参考答案：C

解析：

第一步，本题考查容斥问题，属于二集合容斥类，用公式法解题。

第二步，共两个兴趣小组，其中80%的学生参加地理兴趣小组、30%的学生参加生物兴趣小组，则有80%+50%-100%=30%的学生同时参加两个兴趣小组共300×30%=90（人）。

因此，选择C 选项。

拓展

题干中的“只”字应去掉，否则无正确答案。

第531题

从所给的四个选项中，选择最合适的一个填入问号处，使之呈现一定的规律性。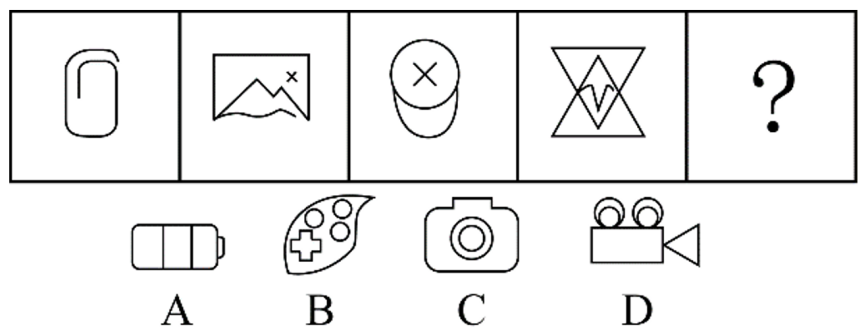

A.A

B.B

C.C

D.D

参考答案：A

解析：

第一步，确定题型。

组成元素不同，优先考虑数量或属性。封闭面特征明显，考虑数面。

第二步，一条式，从左到右找规律。每个图形封闭空间特征明显，考虑数面，题干图形中面的个数为0、1、2、3，所以问号处的图形应选择有4 个面的图形，只有A 项符合。

因此，选择A 选项。

第532题

从所给的四个选项中，选择最合适的一个填入问号处，使之呈现一定的规律性。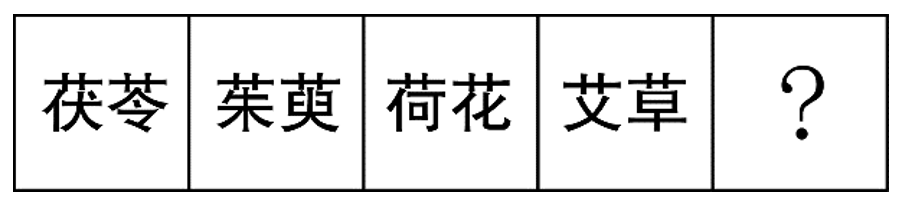

A.地黄

B.菖蒲

C.山药

D.苦笋

参考答案：B

解析：第一步，确定题型。
图形组成相似，优先考虑样式。
第二步，一条式，从左到右找规律。
图形均由两个汉字构成，同时观察每个图形中两个汉字均存在“艹”，考虑整体求同，选择两个汉字均存在“艹”的选项。
因此，选择B 选项。

第533题

从下列四个图形中，找出一个和其他三个具有不同规律的图形。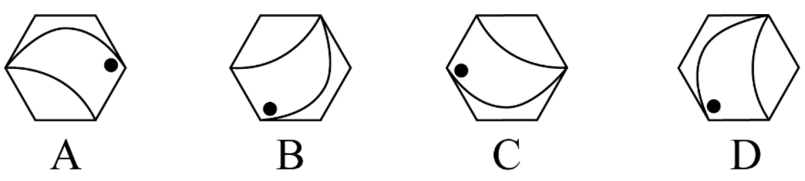

A.A

B.B

C.C

D.D

参考答案：D

解析：第一步，确定题型。
组成元素相同，考虑位置类。
第二步，从左到右找规律。
进行图形之间差异比较，可知前三个为旋转，D 为翻转。
因此，选择D 选项。

第534题

从下列四个图形中，找出一个和其他三个具有不同规律的图形。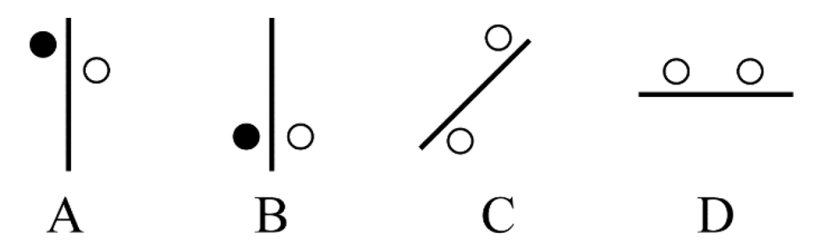

A.A

B.B

C.C

D.D

参考答案：D

解析：

第一步，观察特征。

每幅图中均有一条直线边上存在两个圆，优先考虑圆的标记功能。第二步，提问方式为“找出具有不同规律的图形”，从左到右找规律。ABC 三项中两个圆分别标记在直线的两侧，D 项两个圆标记在直线的同一侧。

因此，选择D 选项。

拓展

本题四个选项中，A 项与B 项都存在一个黑色圆与白色圆，C 项和D 项存在两个白色圆，故本道题并不能从圆的颜色特征找出不同规律。

第535题

从所给的四个选项中，选择最合适的一个填入问号处，使之呈现一定的规律。

A.A

B.B

C.C

D.D

参考答案：D

解析：

第一步，观察特征。

题干图形均由外图圆形与内部方形拼接而成，主要呈现为图形摆放的位置不同，考虑动态位置平移。

第二步，一条式，从左到右找规律。

内部方形按逆时针的顺序依次在右、上、左、下与外部圆形点连接，按照这样的规律，只有D 符合规律。

因此，选择D 选项。拓展

注：三角形与内部线条的交点数量依次为0、1、2、3，所以问号处的图形中内部三角形和正方形的交点数量应为4，只有D 项符合。

第536题

从下列四个图形中，找出一个和其他三个具有不同规律的图形。

A.A

B.B

C.C

D.D

参考答案：B

解析：第一步，观察特征。
组成元素不同，优先考虑数量或属性。
第二步，提问方式为“找出具有不同规律的图形”，从左到右找规律。
选项A、C、D 三个图形均为轴对称图形，选项B 是不对称图形，按照这个规律，选项B 与其他图形规律不一致。
因此，选择B 选项。
拓展
规律二：本题从部分数的角度考虑，只有A 项是2 部分，因此选择A 选项。
规律比较：规律一更有人为设置干扰的倾向。所以优先考虑对称性，选择B 选项。

第537题 从所给的四个选项中，选择最合适的一个填入问号处，使之呈现一定的规律性。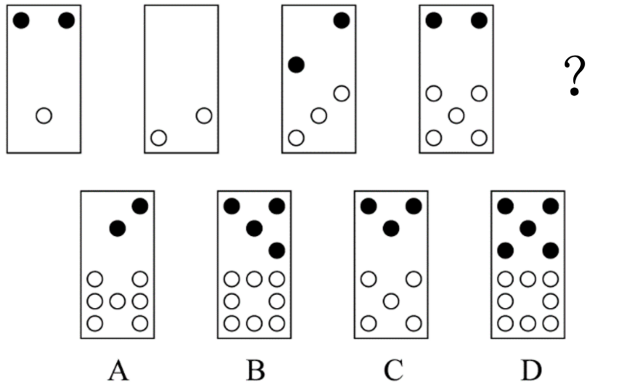

A.A

B.B

C.C

D.D

参考答案：B

解析：第一步，确定题型。
组成元素不同，优先考虑数量类或属性类。图形中黑点与白点数量特征明显，考虑数黑点与白点的数量。
第二步，一条式，从左到右找规律。
图一和图二中的黑点和白点的数量分别相加等于图三中黑点和白点的数量，图二和图三中的黑点和白点的数量分别相加等于图四中黑点和白点的数量，依此规律，图三和图四中的黑点和白点的数量分别相加等于问号处图形中黑点和白点的数量，只有B 项符合。
因此，选择B 选项。

第538题

从所给的四个选项中，选择最合适的一个填入问号处，使之呈现一定的规律性。

A.A

B.B

C.C

D.D

参考答案：B

解析：第一步，确定题型。
组成元素相同，局部元素方向发生变化，考虑旋转和翻转。
第二步，九宫格，横向规律较为常见，优先考虑。
第一行，图1 顺时针旋转180°得到图2，图2 左右翻转得到图3；第二行验证符合此规律；第三行应用规律，图2 左右翻转得到B 项。
因此，选择B 选项。

第539题

下列立体图形，其视图（正视图、俯视图、侧视图）不可能是所给四个选项中的哪一项？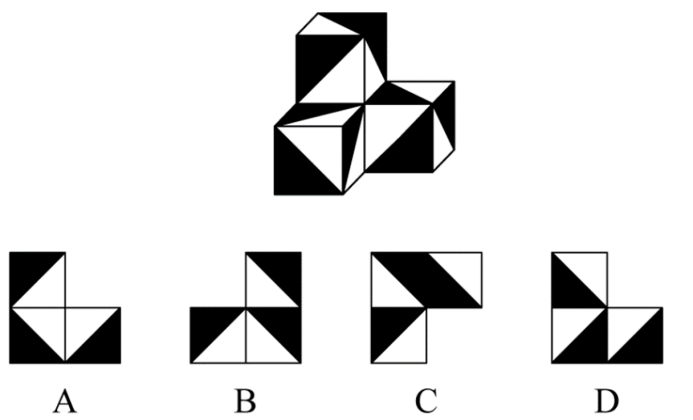

A.A

B.B

C.C

D.D

参考答案：D

解析：第一步，明确设问内容。
选择在任意角度都不能看到的选项。
第二步，分析选项。
A、B、C 项分别为该立体图形的主视图、右视图和俯视图，D 项在任何角度都无法观察得到。
因此，选择D 选项。

第540题

从所给的四个选项中，选择最合适的一项填入问号1和问号2处，使之具有一定规律。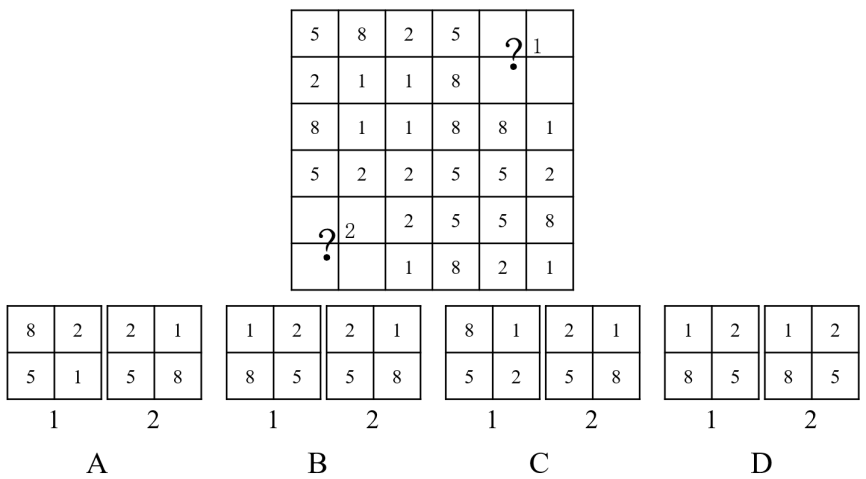

A.A

B.B

C.C

D.D

参考答案：D

解析：

第一步，观察特征。
每个2×2 的格子中均由1、2、5、8 组成，数字位置不同，考虑动态位置类平移。
第二步，将每个2×2 的格子看做一个整体，则为九宫格形式，每一行和每一列的数字均没有规律，整体观察。
经过观察发现，处在组合九宫格外侧的八个图形中，从左上角顺时针观察相邻的两个图形，发现四个数字均顺时针移动一个位置，所以问号1 处的数字应是其左侧的四个数字顺时针移动一个位置得到的，问号2 处的数字应是其右侧的四个数字顺时针旋转一个位置得到的，只有D 项符合。

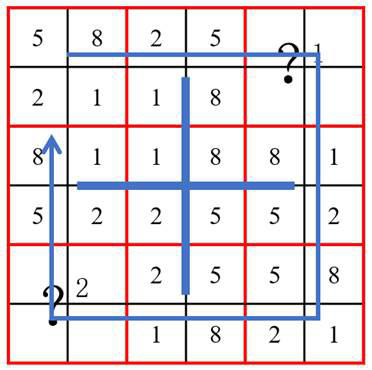
因此，选择D 选项。
拓展
注：中间位置上的数字可以看做是由其上方的四个数字上下翻转得到的，或由其左侧的四个数字左右翻转得到的。