第121题

条形图是利用宽度相同的条形的（ ）来表述数据多少的图形。

A.面积

B.高度或长度

C.频数

D.类别

参考答案：B

解析：

条形图是利用宽度相同的条形的高度或长度来表述数据多少的图形。

第122题

已知某中学课外兴趣小组8个学生的身高分别为（单位：cm）：172、165、169、174、170、173、168、179，则这些学生身高的中位数为()。

A.4

B.4.5

C.172

D.171

参考答案：D

解析：

将身高数据排序为：165、168、169、170、172、173、174、179，因此中位数为(170+172)/2 =171(cm).

第123题

频数分布表中落在某一特定类别的数据个数称为（ ）。

A.组数

B.频数

C.众数

D.中位数

参考答案：B

解析：

频数分布表中落在某一特定类别的数据个数称为频数。

第124题

组距是指每个组变量值中的（ ）。

A.最大值与最小值之差

B.最大值与组中值之差

C.组中值与最小值之差

D.组中值与众数值之差

参考答案：A

解析：

组距=上限-下限

第125题

如果一个数据的标准分数是-3，表明该数据()。

A.比平均数高出3个标准差

B.比平均数低3个标准差

C.等于3倍的平均数

D.等于3倍的标准差

参考答案：B

解析：

如果一个数据的标准分数是-n，表明该数据比平均数低n个标准差。

第126题

若需要比较多个样本不同变量之间的结构差异，可采用的图形为（ ）。

A.条形图

B.饼图

C.环形图

D.频数分布表

参考答案：C

解析：

饼图只能显示一个样本（或总体）各组成部分所占的比重，而环形图可以反映多个样本（或总体）之间的结构差异。

第127题

一个总体的差异程度不仅受标准差大小的影响，而且还受数据本身数值大小的影响。() 

参考答案：对

解析：

差异程度即离散程度，与标准差及平均数的大小有关。

第128题

在一个统计样本中，标准差越大，表明各个观测值分布的越分散。（ ）

参考答案：对

解析：

在一个统计样本中，标准差越大，表明各个观测值分布的越分散，它的趋中程度就越差。

第129题

加权算术平均中权数的实质是()。

A.各组的单位数

B.总体单位数

C.各组的单位数占总体单位数的比重

D.各组的单位数与标志值的乘积

参考答案：C

解析：

加权算术平均数的计算公式为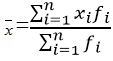：故权数的实质是各组的单位数占总体单位数的比重。

第130题

对于严重偏态分布的数据，平均数比中位数和众数的代表性要好。() 

参考答案：错

解析：

平均数易被多数人理解和接受，实际中用的也较多，但主要缺点是更容易受少数极端数值的影响，对于严重偏态分布的数据，平均数的代表性较差。

第131题

某班共有60名学生，在期末的统计学考试中，男生的平均考试成绩为75分，标准差为6分；女生的平均考试成绩为80分，标准差为6分。如果该班的男女学生各占一半，则全班的平均考试成绩为()。

A.65

B.75.5

C.77.5

D.80

参考答案：C

解析：

设男生成绩为x，女生成绩为y，男女各30人，故全班的平均考试成绩为：

第132题

加权算术平均数的大小()。

A.主要受各组标志值大小的影响，而与各组次数的多少无关

B.主要受各组次数多少的影响，而与各组标志值的大小无关

C.既受各组标志值大小的影响，又受各组次数多少的影响

D.既与各组标志值大小无关，又与各组次数多少无关

参考答案：C

解析：

加权算术平均数计算公式为：因此，决定加权算术平均数大小的因素有两个：①各组标志值的大小；②权数的影响。权数对算术平均数的影响，不取决于权数本身数值的大小，而是取决于作为权数的各组次数占总体次数的比重的大小。各组次数占总体次数的比重是计算加权算术平均数的实质权数。

第133题

描述性统计是研究如何利用样本数据来推断总体特征的统计学方法。（ ） 

参考答案：错

解析：

推断统计是研究如何利用样本数据来推断总体特征的统计学方法。 

第134题

某高校学生上网时间的差异很大，因此宜采用()反映学生上网时间的平均水平。

A.平均数

B.中位数

C.众数

D.极差

E.离散系数

参考答案：BC

解析：

A项，平均数，即是一组数据相加后除以数据的个数得到的结果。平均数易受极端值的影响，而题中该高校学生上网时间差异很大，因此不宜采用。BC两项，中位数，它是数据按照大小排列之后位于中间的那个数（如果样本量为奇数），或者中间两个数目的平均（如果样本量为偶数）；众数，就是数据中出现次数或出现频率最多的数值。二者是位置代表值，均不受极端值影响。DE两项，极差和离散系数是对数据离散程度的度量，不能反映学生上网时间的平均水平。

第135题

下列哪个指标不能反映定性数据的集中趋势（ ）。

A.众数

B.中位数

C.平均数

D.百分比

参考答案：C

解析：

平均数主要用于反映数值型数据的集中趋势。

第136题

某地区 2017 年居民的月平均收入为 5200 元，标准差为 2000 元，则该地区居民收入的离散系数为(     )。

A.2.6

B.0.385

C.0.15

D.0.27

参考答案：B

解析：

离散系数＝标准差/平均数＝2000/5200＝0.385

第137题

在加权算术平均数公式中，若各个变量值都扩大3倍，而频数都减少为原来的1/3，则平均数()。

A.不变

B.减少3倍

C.扩大3倍

D.扩大4倍

参考答案：C

解析：

假设原来的加权算术平均数为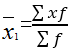若变量值都扩大3倍，而频数都减少为原来的1／3，那么，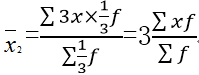

第138题

学生考试成绩60分为及格，不足60分为不及格，这一计分规则体现了统计分组中“上组组限不在其内”的原则。() 

参考答案：对

解析：

学生考试成绩60分为及格，不足60分为不及格，这一计分规则体现了统计分组中“上组组限不在其内”的原则。

第139题

下列关于数据分组的说法，正确的有()。

A.数据分组的组数一般与数据本身的特点及数据的多少有关

B.对于数据分组的组数并没有什么要求，可以任意分组

C.一般情况下，一组数据所分的组数不应少于5组且不多于15组

D.如果组数太少，数据的分布就会过于集中

E.一般情况下，一组数据所分的组数应大于10组

参考答案：ACD

解析：

B项：数据分组的组数一般与数据本身的特点及数据的多少有关;

E项：一般情况下，一组数据所分的组数不应少于5组且不多于15组;

第140题

若数据的分布比较均匀，应编制()。

A.异距数列

B.等距数列

C.单项数列

D.组距数列

参考答案：B

解析：

确定组距时，在研究的现象变动比较均匀的情况下，可以采用等距分组；而当研究的现象变动很不均匀时，例如急剧的增长或急剧的下降，波动的幅度很大时，则一般采用不等距分组。