“微信扫一扫”进入考试题库练习及模拟考试
六年级数学上册单元提优精选题汇编人教版(484题)
第421题 根据3×4=12、33×34=1122、333×334=111222,推测3333×3334=( )
A.11111222
B.11122222
C.11112222
D.11111112
参考答案:C
解析:
解:根据观察知:因数有3的个数与积中1的个数和2的个数相同.
3333×3334=11112222.
故选:C.
第422题 有一列数按如下方式排列:2,4,6,8,10……x,□……那么方框里应填( )
A.x+2
B.2x
C.y
参考答案:A
解析:
解:□里面的前一个数是x,则□里面应填:x+2.
故选:A.
第425题 2×9=18,22×99=2178,222×999=221778,2222×9999=22217778,222222×999999=( )
A.2222177778
B.222221777778
C.22222217777778
D.2222222177777778
参考答案:B
解析:
解:根据分析可得
222222×999999=222221777778
故选:B.
第426题
将一些小圆球如图摆放,第6幅图有( )个小圆球.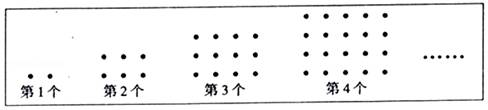
A.30
B.42
C.56
参考答案:B
解析:
解:观察图形可知:
第一个图形中有1×2=2个小圆球,
第二个图形中有2×3=6个小圆球,
第三个图形中有3×4=12个小圆球,
第四个图形中有4×5=20个小圆球,
…
所以第六幅图有6×7=42个小圆球.
故选:B.
第427题
寒假的时候,同学们去莲花山滑雪场滑雪,有些同学用雪杖摆成了如图: 像上面那样摆10个三角形,至少需要( )根滑雪杖.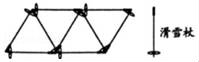
A.21
B.20
C.9
D.30
参考答案:A
解析:
解:摆1个三角形,需要滑雪杖:3根
摆2个三角形,需要滑雪杖:3+2=5(根)
摆3个三角形,需要滑雪杖:3+2+2=7(根)
……
摆n个三角形,需要滑雪杖:3+2(n﹣1)=(2n+1)根
……
摆10个三角形需要滑雪杖:
2×10+1
=20+1
=21(根)
答:摆10个三角形,至少需要21根滑滑雪杖.
故选:A.
第428题
填在下面各正方形中的四个数之间都有相同的规律,根据此规律,n等于( )
A.52
B.74
C.86
参考答案:C
解析:
解:右上角的数:8+2=10
左下角的数:6+2=8
所以n=6+10×8
=6+80
=86
故选:C.
第429题
将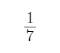 化成小数,那么小数点后的第1993位的数字是( ),此1993个数字之和等于( ).
化成小数,那么小数点后的第1993位的数字是( ),此1993个数字之和等于( ).
参考答案:1;8965
解析:
那么小数点后的第1993位的数字是( 1 ),此1993个数字之和等于( 8965 ).
解:因为 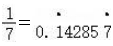 ,1993÷6=332…1.因为循环节的第一位数字是1,故第1993位是1;
,1993÷6=332…1.因为循环节的第一位数字是1,故第1993位是1;
这1993个数字之和为:(1+4+2+8+5+7)×332+1=27×332+1=8965.
第430题 按规律填数:1,8,27,( ),125,( )
参考答案:64;216
解析:
1,8,27,( 64 ),125,( 216 )
解:43=64
63=216
所以:1,8,27,64,125,216.
故答案为:64、216.
第431题
用同样长的小棒摆出如图的图形,照这样继续摆,摆第6个图形用了( )根小棒.
参考答案:25
解析:
解:摆第1个图形需要小棒5根
摆第2个图形需要小棒:5+4=9(根)
摆第3个图形需要小棒:5+4+4=13(根)
……
摆第n个图形需要小棒:5+4(n﹣1)=(4n+1)根
摆第6个图形需要小棒:
4×6+1
=24+1
=25(根)
答:摆第6个图形用了25根小棒.
故答案为:25.
第432题 10.1÷11商的小数部分第100位上的数字是( ).
参考答案:1
解析:
解:10.1÷11=0.9181818…
观察可知双数位上永远是1,第100位是双位数,所以10.1÷11商的小数部分第100位上的数字是1.
故答案为:1
第433题
用小棒按一定的规律摆八边形(如图所示) (1)如果摆成7个八边形,需要( )根小棒. (2)如果想摆n个八边形,需要( )根小棒.
参考答案:50;(7n+1)
解析:
(1)如果摆成7个八边形,需要( 50 )根小棒.
(2)如果想摆n个八边形,需要( (7n+1) )根小棒.
解:摆1个八边形需要小棒:8根
摆2个八边形需要小棒:8+7=15(根)
摆3个八边形需要小棒:8+7+7=22(根)
……
(1)摆7个八边形需要小棒:
8+7×(7﹣1)
=8+42
=50(根)
答:摆成7个八边形,需要50根小棒.
(2)摆n个八边形需要小棒:
8+7(n﹣1)=(7n+1)根
答:摆n个八边形,需要(7n+1)根小棒.
故答案为:50;(7n+1).
第434题
有趣的算式. 4×9=36 44×9=396 444×9=3996 4444×9=39996 44444×9=( ) 444444×9=( )
参考答案:399996;3999996
解析:
解:4×9=36
44×9=396
444×9=3996
4444×9=39996
44444×9=399996
444444×9=3999996
故答案为:399996;3999996.
第435题
下面的算式是按规律排列的: 1+1,2+3,3+5,4+7,1+9,2+11,3+13,4+15,1+17,… 第( )个算式中的得数是2013.
参考答案:1006
解析:
解:由分析可知:因为2013是奇数,2个加数中第二个一定是奇数,所以第一个必为偶数,所以是2或4,如果是2:那么第二个数为2013﹣2=2011,2011是第(2011+1)÷2=1006项,而数字2始终是偶,两者相符,所以这个算式是2+2011,是第1006个算式.
故答案为:1006.
第436题
按规律填空. 21×9=189 321×9﹣2889 4321×9=38889 54321×9=( ) … ( )×9=8888888889
参考答案:488889;987654321
解析:
解:21×9=189
321×9=2889
4321×9=38889
54321×9=488889
…
987654321×9=8888888889
规律:一个因数是9,另一个因数是从1开始的整数倒序排列,积的个位是9,前面数位上的数字是8,8的个数是整数的个数减1;最高位是整数的个数减1的数.
故答案为:488889;987654321.
第438题 按1、8、27、( ) 、125、216的规律排,横线中的数应为64. (判断对错)
参考答案:对
解析:
解:13=1;23=8;33=27;43=64;53=125; 63=216.
由此发现规律:以上数列是按1、2、3、4、5、6的立方顺序排列的,43=64.
故答案为:正确.
第439题 根据33×4=132,333×4=1332,3333×4=13332,可知33333×4=133332. (判断对错)
参考答案:对
解析:
解:33×4=132,
333×4=1332,
3333×4=13332,
可知:33333×4=133332.
原题说法正确。
故答案为:√.
第440题
如图,第五个点阵中点的个数是17个. (判断对错)
参考答案:对
解析:
解:第一个点阵中点的个数:1个
第二个点阵中点的个数:1+4=5(个)
第三个点阵中点的个数:1+4+4=9(个)
……
第n个点阵中点的个数:1+4(n﹣1)=(4n﹣3)(个)
……
第五个点阵中点的个数:
4×5﹣3
=20﹣3
=17(个)
答:第五个点阵中点的个数是17个.所以原说法正确.
故答案为:√.
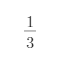 ,第二次锯掉余下的
,第二次锯掉余下的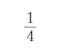 ,第三次锯掉余下的
,第三次锯掉余下的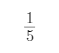 ……,第六次锯掉余下的
……,第六次锯掉余下的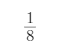 后,这根木条还剩( )
后,这根木条还剩( )