
“微信扫一扫”进入题库练习及模拟考试
初中数学八年级上册试题库(555题)
我们学过完全平方公式:
…….我们将其系数排列可以得到系数具有如下规律:
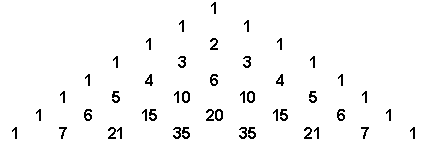
我们称此为杨辉三角形,它表明了底数是两项式的n次方的展开式中系数的规律。
探究规律,写出
知识点:第十四章 整式的乘法与因式分解
参考答案:\({2^n}\)

“微信扫一扫”进入题库练习及模拟考试
我们学过完全平方公式:
…….我们将其系数排列可以得到系数具有如下规律:

我们称此为杨辉三角形,它表明了底数是两项式的n次方的展开式中系数的规律。
探究规律,写出
参考答案:\({2^n}\)